Todd-Coxeter 算法和 3D/4D 均匀多胞体
本文介绍我写的一个高颜值的、脱离了低级趣味的小程序:用 Python 和 POV-Ray 绘制各种三维多面体和四维多胞体,代码在 Github 上。
以下是用这个程序渲染的一些例子,其中不同颜色的顶点/边/面表示它们在对称群的作用下位于不同的轨道中,具体解释见后。
例子
所有的 Platonic 多面体,Archimedean 多面体,比如 snub dodecahedron:
所有的 Kepler-Poinsot 多面体,比如 great icosahedron:
所有的四维均匀多胞体 (除去一个特例 The grand antiprism),比如我的 Github 头像 (runcinated 120-cell):

截断的四维正方体 truncated tesseract:
4d cube:

也可以是非凸的,比如星状正多胞体中的 grand stellated 120-cell:
甚至是 5 维欧氏空间中的均匀多胞体,如 5-cube:
等等,可玩的效果是非常多的。
以上这些都是在 Python 中做好计算以后,将多胞体的数据导出到 POV-Ray 中渲染得到的。你完全可以通过改写代码中的 POV-Ray 的部分来渲染得出不同的效果,当然前提是需要掌握 POV-Ray 的场景描述语言,不过这属于另一段故事,就不在本文的讨论范围内了。
下面介绍程序背后的数学原理。
这些图画的都是什么?
这些图都是三维或者四维欧氏空间中凸/非凸的均匀多胞体 (polytope),三维的情形更常用的称呼是多面体。这里有几个关键词需要注意:凸/非凸、均匀。
凸比较好理解,就是指多胞体上任意两点间的连线仍然属于此多胞体,否则就是非凸。上面的例子中 Platonic 多面体、Archimedean 多面体都是凸的;但 Kepler-Poinsot 多面体、星状正多胞体都是非凸的。
均匀这个词就不太好理解了。简单说就是:多胞体的所有顶点都一样,且每个二维的面都是正多边形,每个三维的胞腔都是均匀多面体(这是个递归的定义)。
要准确解释什么叫所有顶点都一样,就要用到群论的语言:一个多胞体 \(P\) 的对称群 \(G\) 是欧氏空间中一组正交变换构成的有限群,\(G\) 作用在 \(P\) 上保持 \(P\) 不变。所有顶点都一样的严格说法是 \(G\) “传递地”作用在 \(P\) 的顶点集上,即对 \(P\) 的任何两个顶点 \(u,v\),都存在 \(g\in G\),\(g\) 把 \(u\) 映射为 \(v\)。
这些图是怎么画出来的?
这些多胞体看起来样子大不相同,但它们都可以用同一种方法计算出来,叫做 Wythoff 构造法,也称万花筒构造法。它的原理跟我们小时候玩的万花筒的原理是一样的:在空间中放置若干过原点的反射平面 (镜子),镜面之间的夹角是精心设计好的,都形如 \(\pi-\pi/p\),其中 \(p\) 为有理数。在空间中选定一个初始顶点 \(v_0\),将 \(v_0\) 关于这些镜子反复作反射变换,得到的全部镜像就是多胞体的顶点。如果 \(v_0\) 关于第 \(i\) 面镜子反射后得到的镜像是 \(v_1\),则 \((v_0,v_1)\) 构成一条类型为 \(i\) 的边,我们把它以及在对称群作用下同轨道的所有边都染成 \(i\) 号色。如果 \(v_0\) 先关于镜面 \(i\) 作反射,再关于镜面 \(j\) 作反射,则由于两个反射变换的复合是一个旋转变换,\(v_0\) 实际上是绕着某个面的中心和原点的连线作了一次旋转,旋转的角度为 \(2\pi/m\) (假设镜面 \(i\) 和镜面 \(j\) 的法向量夹角是 \(\pi-\pi/m\)),重复此旋转 \(m\) 次即可得到多胞体的一个类型为 \((i,j)\) 的面,我们把它在对称群作用下同轨道的所有面都染成同一颜色。
这里的关键问题有两个:
- 对于不同的均匀多胞体,应该如何放置这些镜面,并选择初始顶点?
- 摆好镜面和初始顶点以后,怎样不重复不遗漏地计算初始顶点的所有镜像?
第一个问题的答案叫做 Coxeter-Dynkin 图,Coxeter-Dynkin 图是一个带标记信息的无向图,它编码了多胞体的全部信息,即只要知道了多胞体对应的 Coxeter-Dynkin 图,就可以求出该多胞体的所有数据 (仅缩放大小和在空间中的摆放位置除外)。每个均匀多胞体都有一个 Coxeter-Dynkin 图与之对应,但是不同的 Coxeter-Dynkin 图可能描述的是相同的多胞体。
比如正方体的 Coxeter-Dynkin 图为:
我们来解释这个图的含义:
在一个 Coxeter-Dynkin 图中,每个顶点代表一面镜子,在上图中有三个顶点,所以有三面镜子。将这三面镜子从左到右依次记作 \(m_0, m_1, m_2\),顶点之间的边记录了镜子间的夹角:
- 若两个镜面之间的夹角为 \(\pi/2\) 则它们之间没有边相连。
- 若两个镜面之间的夹角为 \(\pi-\pi/3\) 则它们之间用一条无标记的边相连。
- 若两个镜面之间的夹角为 \(\pi-\pi/m\) (\(m\) 为有理数且 \(m>2, m\ne3\)),则它们之间用一条标号为 \(m\) 的边相连。
此外用圈出的镜面来标记初始顶点的位置,一个镜面被圈出当且仅当初始顶点不在这个镜面上。
从而在正方形的情形 \(\langle m_0,m_1\rangle=\pi-\pi/4\),\(\langle m_1,m_2\rangle=\pi-\pi/3\),\(\langle m_0,m_2\rangle=\pi/2\)。初始顶点落在 \(m_1\) 和 \(m_2\) 上但是不属于 \(m_0\)。
于是这三面镜子可以这样摆放:
- 镜子 \(m_0\) 的法向量可以随意,比如 \(n_0=(1, 0, 0)\)。
- 镜子 \(m_1\) 的法向量 \(n_1\) 与 \(n_0\) 夹角为 \(3\pi/4\),于是 \(n_1\) 可以取为 \((\cos\dfrac{3\pi}{4}, \sin\dfrac{3\pi}{4}, 0)\)。
- 镜子 \(m_2\) 的法向量 \(n_2\) 与 \(n_0\) 垂直,所以 \(n_2\) 形如 \((0,y_3,z_3)\),它与 \(n_1\) 夹角是 \(2\pi/3\),所以 \(y_3 \sin\dfrac{3\pi}{4}=\cos\dfrac{2\pi}{3}\),再结合 \(n_2\) 是单位向量,\(z_3=\sqrt{1-y_3^2}\),解出 \(y_3, z_3\) 即可。
要选择一个落在 \(m_1\) 和 \(m_2\) 上但是不落在 \(m_0\) 上的初始点 \(v_0\),我们可以让 \(v_0\) 到平面 \(m_1\) 和 \(m_2\) 的距离为 0,到平面 \(m_0\) 的距离为 1,即
\[\langle v_0, n_0\rangle=1,\quad \langle v_0, n_1\rangle=0,\quad\langle v_0, n_2\rangle=0.\]
求解这个线性方程组即可。
我们前面提到过,要使得初始顶点的所有镜像恰好构成一个均匀多胞体,镜子之间的夹角必须精心设置,这实际上只有有限种可能。换句话说,只有有限个 Coxeter-Dynkin 图可以给出 3D/4D 的均匀多胞体。在 维基百科 上完整的列出了每种均匀多胞体对应的 Coxeter-Dynkin 图,这里就不再专门列举了,但是特别指出两点:
- Coxeter-Dynkin 图的标号完全决定了多胞体的对称性,而初始顶点的位置则决定了多胞体的截断类型。
- 对偶的多胞体具有相同的 Coxeter-Dynkin 图,只不过要把边的标号从右到左反过来。比如正八面体和正方体的 Coxeter-Dynkin 图是一样的,但是边的标号是 (3, 4)。
第二个问题的答案叫做 Todd-Coxeter 算法,展开讲的话比较复杂,我们单列一节专门谈谈。
有限表现群和 Todd-Coxeter 算法
怎样求出初始顶点在所有镜子中的镜像?有个简单的办法:只要反复地将初始顶点关于每个镜面作反射,算出得到的镜像点的坐标,并与之前得到的点的坐标相比较(浮点数比较需要在一定的误差范围内考虑),直到不再有新的镜像点出现为止,不就得到全部顶点集吗?这个方法确实可行,但是既笨又丑陋:它完全没有用到多胞体具有对称性这一事实!
这个程序采用的是基于符号计算的途径,这个方法可以精准地得出所有顶点/边/面的信息,代价就是涉及的数学略复杂。我们先回忆一下群在集合上的作用的轨道—稳定化子定理:
轨道 — 稳定化子定理. 设群 \(G\) 传递地作用在集合 \(S\) 上,设 \(x\in S\) 的稳定化子群是 \(H\),则集合 \(S\) 与 \(G/H\) 中的右陪集之间有一一对应:\(x\cdot g\leftrightarrow Hg\)。
注: 和一般的约定不同,这里群在集合上的作用为作用在右边,主要是为了编程方便,实际上左边右边都一样。
这个定理告诉我们,如果群 \(G\) 传递地作用在一个集合 \(S\) 上,而且对 \(S\) 中某个元素 \(x\) 我们知道了它的稳定化子群 \(H\),则只要对 \(G/H\) 的每个陪集代表元 \(g\),将 \(g\) 作用在 \(x\) 上就可以得到整个 \(S\)。
于是给定一个均匀多胞体 \(P\),要求出其全部顶点集合,我们只要:
- 根据 \(P\) 的 Coxeter-Dynkin 图确定其对称群 \(G\) 和初始顶点 \(v_0\)。
- 定出 \(v_0\) 的稳定化子群 \(H\) 并求出 \(G/H\) 的一组陪集代表元。
- 将 \(G/H\) 中的每个陪集代表元作用在 \(v_0\) 上即得 \(P\) 的全部顶点。
我们仍然以正方体为例来讲解:正方体的 Coxeter-Dynkin 图是
仍然记三个镜面为 \(m_0,m_1,m_2\),其法向量分别为 \(n_0,n_1,n_2\),设 \(\rho_0,\rho_1,\rho_2\) 分别是关于它们的反射变换,\(\rho_i\) 对应的矩阵为 \(M_i=I-2n_in_i^T\)(见 Householder 变换)。
正方体的对称群 \(G\) 由 \(\rho_0,\rho_1,\rho_2\) 这三个基本反射生成,其表现为: \[G = \langle\rho_0,\rho_1,\rho_2\ |\ \rho_0^2=\rho_1^2=\rho_2^2=(\rho_0\rho_1)^4=(\rho_1\rho_2)^3=(\rho_0\rho_2)^2=1\rangle.\] 这是因为反射的平方总是恒等变换,所以 \(\rho_i^2=1\)。\(\rho_0,\rho_1\) 是两个夹角为 \(3\pi/4\) 的反射,所以 \(\rho_0\rho_1\) 是一个角度为 \(3\pi/2\) 的旋转,旋转轴为 \(m_0\) 和 \(m_1\) 的交线,从而 \((\rho_0\rho_1)^4=1\)。\(\rho_1\rho_2,\rho_0\rho_2\) 的情形是类似的。1
利用 Todd-Coxeter 算法 (后面有解释) 不难求出这个群包含 48 个元素,罗列如下: \[\begin{array}{lll}e&\rho_{0}&\rho_{0}\rho_{1}\\ \rho_{0}\rho_{1}\rho_{0}&\rho_{0}\rho_{1}\rho_{0}\rho_{1}&\rho_{1}\rho_{0}\rho_{1}\\\rho_{1}\rho_{0}&\rho_{1}&\rho_{0}\rho_{2}\\\rho_{2}&\rho_{1}\rho_{2}&\rho_{1}\rho_{2}\rho_{1}\\\rho_{2}\rho_{1}&\rho_{0}\rho_{1}\rho_{2}&\rho_{0}\rho_{1}\rho_{2}\rho_{1}\\\rho_{0}\rho_{2}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\\\rho_{0}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}&\rho_{1}\rho_{0}\rho_{1}\rho_{2}\\\rho_{1}\rho_{0}\rho_{2}&\rho_{1}\rho_{0}\rho_{2}\rho_{1}&\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\\\rho_{2}\rho_{1}\rho_{0}&\rho_{2}\rho_{1}\rho_{0}\rho_{1}&\rho_{0}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\\\rho_{0}\rho_{2}\rho_{1}\rho_{0}&\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}&\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\\\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}&\rho_{1}\rho_{2}\rho_{1}\rho_{0}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\\\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\rho_{1}&\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}&\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\\\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}&\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\\\rho_{0}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}&\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}&\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\\\rho_{0}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}&\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}&\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\\\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\end{array} \] 由于在正方形的 Coxeter-Dynkin 图中只有镜面 \(m_0\) 是被圈出的,即初始顶点 \(v_0\) 落在 \(m_1\) 和 \(m_2\) 上,但不属于 \(m_0\),所以反射 \(\rho_1,\rho_2\) 保持 \(v_0\) 不动,\(\rho_0\) 将 \(v_0\) 映射为其关于 \(m_0\) 的镜像,于是 \(v_0\) 的稳定化子群是 2 \[H=\langle \rho_1, \rho_2\ |\ \rho_1^2=\rho_2^2=(\rho_1\rho_2)^3=e\rangle.\] 显然 \(H\) 就是二面体群 \(D_3\),所以 \(|H|=6\),从而 \(|G/H|=8\)。利用 Todd-Coxeter 算法可得其一组右陪集代表元为 \[\begin{array}{llll}e&\rho_{0}&\rho_{0}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\\\rho_{0}\rho_{1}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\end{array} \] 将它们作用在 \(v_0\) 上即可得到正方体的 8 个顶点。例如 \(\rho_0\rho_1\) 作用在 \(v_0\) 上为 \[v_0(\rho_0\rho_1)=(v_0\rho_0)\rho_1=(v_0M_0)\rho_1=v_0M_0M_1.\] 其中 \(v_0\) 写成行向量的形式,每个 \(M_i\) 是对称矩阵。
计算边/面/胞腔的原理是类似的,但考虑的细节要多一些。比如我们想求出所有关于第 \(i\,(i=0,1,2)\) 个镜面 \(m_i\) 反射生成的类型为 \(i\) 的边,可以这样做:
- 检查初始顶点 \(v_0\) 是否落在 \(m_i\) 上。如果答案为是,那么关于此镜面的反射保持 \(v_0\) 不变,此多面体不含类型 \(i\) 的边。否则设 \(v_0\) 关于 \(m_i\) 的镜像为 \(v_1\),则 \((v_0, v_1)\) 构成一条类型为 \(i\) 的边 \(e\)。
- 关于 \(m_i\) 的反射 \(\rho_i\) 把 \(v_0\) 和 \(v_1\) 互换,从而保持 \(e\) 不变。注意其它任何与 \(m_i\) 垂直并且包含初始点 \(v_0\) 的镜面反射也会保持 \(e\) 不变。在正方形的情形中,反射 \(\rho_0\) 互换 \(e\) 的两端因而保持 \(e\) 不变,此外镜面 \(m_0\) 和 \(m_2\) 是垂直的,且 \(v_0\) 包含在 \(m_2\) 中,所以反射 \(\rho_2\) 保持 \(e\) 上的每个点不变,于是 \(e\) 的稳定化子群为 \(H=\langle \rho_0,\rho_2 \rangle\)。显然 \(H\) 同构于 \(\mathbb{Z}_2\times\mathbb{Z}_2\),所以 \(|H|=4\),从而 \(|G/H|=12\),即正方体有 12 条边 3。
- 求出 \(G/H\) 的一组陪集代表元并作用在 \(e\) 上得出全部类型为 \(i\) 的边。
求面的情形复杂一些,基本原理是这样的:
- 对 \(i\ne j\),如果初始顶点 \(v_0\) 不同时属于镜面 \(i\) 和镜面 \(j\),则旋转 \(\rho_i\rho_j\) 就可以生成一个面 \(f\)。需要注意的是,如果这两个镜面恰好垂直,则必须二者均不包含 \(v_0\) 才能得到一个非退化的面,这个面是个正方形。在正方体的情形,\(\rho_0\rho_1\) 可以生成一个面,\(\rho_0\rho_2\)(两镜面垂直但只有一个镜面包含 \(v_0\))和 \(\rho_1\rho_2\)(两镜面均包含 \(v_0\))都不能给出面。
- \(f\) 的稳定化子群是由 \(\rho_i,\rho_j\) 和那些包含 \(v_0\) 且与 \(m_i,m_j\) 均垂直的镜面反射生成。在正方形的情形是 \(H=\langle \rho_0,\rho_1 \rangle\) 4,显然 \(H\) 同构于二面体群 \(D_8\),因此 \(|H|=8\),\(|G/H|=6\),即正方体有 6 个面。
总之关键的步骤都是给定群 \(G\) 和某个子群 \(H\),求 \(G/H\) 的一组陪集代表元。
这里用到的算法叫做 Todd-Coxeter 算法。
Todd-Coxeter 算法在许多抽象代数或者群论的教材都有,用到的数学知识并不复杂。但完整描述并证明一份程序实现的细节还是很费功夫的,恐怕要好几页纸才能说清楚。限于篇幅,我这里仅用正方体的情形为例说明算法的步骤,具体的证明和更多的细节读者请参考
Handbook of Computational Group Theory, Holt, D., Eick, B., O’Brien, E.
中的 coset enumeration 一章。我个人认为这是讲解 Todd-Coxeter 算法最棒的文献。
Todd-Coxeter 算法非常类似玩数独游戏,这里要填的表是一个变化的二维数组 \(T\),\(T\) 的行 \(i\) 代表第 \(i\) 个右陪集,\(T\) 的列 \(j\) 代表第 \(j\) 个生成元 \(\rho_j\),\(T[i][j]\) 的值等于 \(\rho_j\) 右乘以第 \(i\) 个陪集后得到的陪集。初始时,我们知道肯定有一个陪集,就是 \(H\) 自身,还有没有其它的陪集我们不清楚。算法的主要流程就是根据 \(G\) 和 \(H\) 的表现中包含的关系来发现新的陪集并填入表中,直到无法找到新的陪集为止。最终得到的 \(T\) 实际上是 \(G/H\) 的 schreier 图的邻接矩阵,它记录了 \(G/H\) 的陪集间的乘法关系,由 \(T\) 出发我们很容易求出这些陪集的 word 表示。
例: 设 \(G\) 是正方体的对称群,其表现为 \[G = \langle\rho_0,\rho_1,\rho_2\ |\ \rho_0^2=\rho_1^2=\rho_2^2=(\rho_0\rho_1)^4=(\rho_1\rho_2)^3=(\rho_0\rho_2)^2=1\rangle.\] 子群 \(H=\langle \rho_1, \rho_2\rangle\) 是初始顶点的稳定化子群,求 \(G/H\) 的一组右陪集代表元。
我们先罗列一下这个数独游戏已知的关系:
已知关系:
- 对 \(H\) 的任何生成字 \(w\) 有 \(H\cdot w=H\),即 \(H\rho_1=H\rho_2=H\)。注意此关系仅要求对 \(H\) 成立。
- 对任何陪集 \(K\) 和 \(G\) 的任何生成关系 \(r\) 有 \(K\cdot r=K\),即 \(K\rho_i^2=K, i=0,1,2\) 以及 \(K(\rho_0\rho_1)^4=K(\rho_1\rho_2)^3=K(\rho_0\rho_2)^2=K\)。注意此关系要求对所有陪集成立。
这些关系可以存储在两个列表里面,每个关系用一个数组表示。
第一个列表存储的是 \(H\) 的生成字,即
\(H\) 的生成字列表:
- (1,)
- (2,)
第二个列表存储的是 \(G\) 的生成关系,即
\(G\) 的生成关系列表:
- (0, 0)
- (1, 1)
- (2, 2)
- (0, 1, 0, 1, 0, 1, 0, 1)
- (1, 2, 1, 2, 1, 2)
- (0, 2, 0, 2)
其中每条关系前面的数字是我们加上的编号以便于称呼。
注: 在非 Coxeter 群的情形还要把每个生成元的逆也作为生成元加入,其在 \(T\) 中也占据一列,所以实际上 \(T\) 的列的个数要 \(\times2\)。但是在 Coxeter 群的情形每个生成元是 2 阶的,其逆元素等于自身,所以不需要额外考虑逆元素。
初始时刻表格 \(T\) 是这样的:
| \(\rho_0\) | \(\rho_1\) | \(\rho_2\) | |
|---|---|---|---|
| \(H_0\) | \(\phantom{}\) | \(\phantom{}\) | \(\phantom{}\) |
其中 \(H_0\) 代表 \(H\) 对应的陪集。程序首先验证 \(H_0\) 所在的行满足第一个关系列表 (\(H\) 的生成字列表,随后此列表可以被丢弃),然后依次从上到下扫描 \(T\) 的每一行,假设当前扫描的是第 \(i\) 行,对应的陪集为 \(H_i\),程序验证确保对第二个列表 (\(G\) 的生成关系列表) 中的每条关系 \(w\),\(H_i\) 满足 \(H_iw=H_i\),这个过程中可能发现新的陪集,也可能发现已有的某些陪集是重复的,也有可能需要强行定义新的陪集来使得这个验证能够完成。
我们来开始扫描 \(H_0\) 所在的行:首先检查第一个列表中的关系,这个列表仅在扫描 \(H_0\) 时使用一次,扫描完就可以丢弃。
(1). 对第 0 条关系 \(H_0\rho_1=H_0\),即 \(T[0][1]=0\)。对第 1 条关系 \(H_0\rho_2=H_0\),即 \(T[0][2]=0\),这时 \(T\) 变成了
| \(\rho_0\) | \(\rho_1\) | \(\rho_2\) | |
|---|---|---|---|
| \(H_0\) | \(\phantom{}\) | 0 | 0 |
第一个列表扫描完毕,接下来扫描第二个列表。
(2). 对第 2 条关系 \(H_0\rho_0^2=H_0\),由于 \(H_0\rho_0\) 还不知道,我们将其定义为新陪集 \(H_1\) 并将 1 填入 \(T[0][0]\) 位置,此外还要为 \(H_1\) 开辟新的一行:
| \(\rho_0\) | \(\rho_1\) | \(\rho_2\) | |
|---|---|---|---|
| \(H_0\) | 1 | 0 | 0 |
| \(H_1\) | 0 | \(\phantom{}\) | \(\phantom{}\) |
注: 每次定义新陪集时,比如定义 \(H_i\rho_j=H_k\),我们同时自动得到了与之对称的关系 \(H_k\rho_j=H_i\rho_j^2=H_i\),因此每次填表时我们都填写一对数字而不是一个,这样可以保证表格 \(T\) 的 “对称性”。
(3). 第 3 条和第 4 条关系已经满足,继续。
(4). 第 5 条关系,\(H_0\rho_0\rho_1\rho_0\rho_1\rho_0\rho_1\rho_0\rho_1=H_0\),我们已经知道 \(H_0\rho_0=H_1\) 但是 \(H_1\rho_1\) 还不知道,将其定义为 \(H_2\),于是 \(T\) 中又添两项,并开辟新的一行给 \(H_2\):
| \(\phantom{}\) | \(\rho_0\) | \(\rho_1\) | \(\rho_2\) |
|---|---|---|---|
| \(H_0\) | 1 | 0 | 0 |
| \(H_1\) | 0 | 2 | \(\phantom{}\) |
| \(H_2\) | \(\phantom{}\) | 1 | \(\phantom{}\) |
但是 \(H_2\rho_0\) 还是不知道,所以继续定义 \(H_2\rho_0=H_3\),于是 \(T\) 变成
| \(\rho_0\) | \(\rho_1\) | \(\rho_2\) | |
|---|---|---|---|
| \(H_0\) | 1 | 0 | 0 |
| \(H_1\) | 0 | 2 | \(\phantom{}\) |
| \(H_2\) | 3 | 1 | \(\phantom{}\) |
| \(H_3\) | 2 | \(\phantom{}\) | \(\phantom{}\) |
于是现在关系变成了
\[\underbrace{\overbrace{\underbrace{H_0\rho_0}_{=H_1}\,\rho_1}^{=H_2}\,\rho_0}_{=H_3}\,\rho_1\rho_0\rho_1\rho_0\rho_1=H_0.\]
但是 \(H_3\rho_1\) 还是不知道,你可能会想把它继续定义为新的陪集 \(H_4\),然后继续扫描。这样做不是不可以,但是每次都定义新陪集会生成大量重复的陪集,导致 \(T\) 增长的非常快,对更复杂的群非常耗费计算资源。我们采用更聪明的办法:倒着扫描整个关系,即从右到左扫描 \(H_0\rho_0\rho_1\rho_0\rho_1\rho_0\rho_1\rho_0\rho_1=H_0\) 这条关系。记住我们现在已经正向 (从左到右) 扫描到了下面的位置: \[\underbrace{H_0\rho_0\rho_1\rho_0}_{=H_3}\,\rho_1|\rho_0\rho_1\rho_0\rho_1=H_0.\] 反向扫描意味着我们把上式左边末尾的 \(\rho_0\rho_1\rho_0\rho_1\) 挪到右边去,变形为 \[\underbrace{H_0\rho_0\rho_1\rho_0}_{=H_3}\,\rho_1=\underbrace{H_0\rho_1}_{=H_0}\rho_0\rho_1\rho_0=H_0\rho_0\rho_1\rho_0= H_3.\] 从而 \(H_3\rho_1=H_3\)。这样通过反向扫描我们就推断出了 \(H_3\rho_1\) 的值,避免了定义冗余的陪集。按照 Holt 书中的说法这叫做一个 deduction。这时 \(T\) 为
| \(\rho_0\) | \(\rho_1\) | \(\rho_2\) | |
|---|---|---|---|
| \(H_0\) | 1 | 0 | 0 |
| \(H_1\) | 0 | 2 | \(\phantom{}\) |
| \(H_2\) | 3 | 1 | \(\phantom{}\) |
| \(H_3\) | 2 | 3 | \(\phantom{}\) |
注: 在实际的程序实现中,我们总是从关系的两头同时开始扫描,直到它们相遇为止。
(5). 关系 6 已经满足,继续。
(6). 对关系 7 \(H_0\rho_0\rho_2\rho_0\rho_2=H_0\),从两头扫描我们得到 \[\underbrace{H_0\rho_0}_{=H_1}\,\rho_2=\underbrace{\overbrace{H_0\rho_2}^{=H_0}\rho_0}_{=H_1}.\] 即 \(H_1\rho_2=H_1\),我们又得到了一个 deduction,从而 \(T\) 变成
| \(\rho_0\) | \(\rho_1\) | \(\rho_2\) | |
|---|---|---|---|
| \(H_0\) | 1 | 0 | 0 |
| \(H_1\) | 0 | 2 | 1 |
| \(H_2\) | 3 | 1 | \(\phantom{}\) |
| \(H_3\) | 2 | 3 | \(\phantom{}\) |
至此对 \(H_0\) 的扫描全部完成,我们转入扫描 \(H_1\) 所在的行。
注意:从现在起至程序结束,我们不再使用第一个列表。
下面开始扫描 \(H_1\) 所在的行。
(1). 经检查关系 2, 3, 4, 5 已经满足,继续。
(2). 对关系 6 有 \(H_1\rho_1\rho_2\rho_1\rho_2\rho_1\rho_2=H_1\),其中 \(H_1\rho_1=H_2\) 已知但 \(H_2\rho_2\) 未知。反向的扫描也会卡在这里: \[\underbrace{H_1\rho_1}_{=H_2}\rho_2\rho_1=H_1\rho_2\rho_1\rho_2=H_2\rho_2.\] 所以我们定义新陪集 \(H_2\rho_2=H_4\),于是 \(H_4\rho_1=H_4\),从而此时 \(T\) 为
| \(\rho_0\) | \(\rho_1\) | \(\rho_2\) | |
|---|---|---|---|
| \(H_0\) | 1 | 0 | 0 |
| \(H_1\) | 0 | 2 | 1 |
| \(H_2\) | 3 | 1 | 4 |
| \(H_3\) | 2 | 3 | \(\phantom{}\) |
| \(H_4\) | \(\phantom{}\) | 4 | 2 |
(3). 关系 7 已经满足,从而 \(H_1\) 检查完毕,接下来开始扫描 \(H_2\) 的行。
下面开始扫描 \(H_2\) 的行。
(1). 经检查关系 2, 3, 4, 5, 6 都已经满足,继续。
(2). 对关系 7 有 \(H_2\rho_0\rho_2\rho_0\rho_2=H_2\),两边同时扫描的结果为: \[\underbrace{H_2\rho_0}_{=H_3}\rho_2\rho_0=H_2\rho_2=H_4.\] 即 \(H_3\rho_2\rho_0=H_4\),但是继续正向扫描 \(H_3\rho_2\) 不知道,继续反向扫描 \(H_4\rho_0\) 不知道。定义新陪集 \(H_3\rho_2=H_5\),于是 \(H_5\rho_0=H_4\),我们又可以填入两对 4 个数字,此时 \(T\) 为:
| \(\rho_0\) | \(\rho_1\) | \(\rho_2\) | |
|---|---|---|---|
| \(H_0\) | 1 | 0 | 0 |
| \(H_1\) | 0 | 2 | 1 |
| \(H_2\) | 3 | 1 | 4 |
| \(H_3\) | 2 | 3 | 5 |
| \(H_4\) | 5 | 4 | 2 |
| \(H_5\) | 4 | \(\phantom{}\) | 3 |
\(H_2\) 扫描完毕,下面扫描 \(H_3\) 的行。
我把 \(H_3, H_4, H_5\) 的扫描过程留给你作为练习,\(H_3\) 扫描结束后你得到的 \(T\) 应该如下图:
| \(\rho_0\) | \(\rho_1\) | \(\rho_2\) | |
|---|---|---|---|
| \(H_0\) | 1 | 0 | 0 |
| \(H_1\) | 0 | 2 | 1 |
| \(H_2\) | 3 | 1 | 4 |
| \(H_3\) | 2 | 3 | 5 |
| \(H_4\) | 5 | 4 | 2 |
| \(H_5\) | 4 | 6 | 3 |
| \(H_6\) | \(\phantom{}\) | 5 | 6 |
\(H_4\) 扫描结束后你得到的 \(T\) 应该如下图:
| \(\rho_0\) | \(\rho_1\) | \(\rho_2\) | |
|---|---|---|---|
| \(H_0\) | 1 | 0 | 0 |
| \(H_1\) | 0 | 2 | 1 |
| \(H_2\) | 3 | 1 | 4 |
| \(H_3\) | 2 | 3 | 5 |
| \(H_4\) | 5 | 4 | 2 |
| \(H_5\) | 4 | 6 | 3 |
| \(H_6\) | 7 | 5 | 6 |
| \(H_7\) | 6 | 7 | \(\phantom{}\) |
\(H_5\) 的扫描给不出新的信息。
扫描 \(H_6\) 时,关系 2, 3, 4, 5, 6 都已经满足,由关系 7 \(H_6\rho_0\rho_2\rho_0\rho_2=H_6\) 可得 deduction \(H_7\rho_2=H_7\),于是 \(T\) 可以补全为
| \(\rho_0\) | \(\rho_1\) | \(\rho_2\) | |
|---|---|---|---|
| \(H_0\) | 1 | 0 | 0 |
| \(H_1\) | 0 | 2 | 1 |
| \(H_2\) | 3 | 1 | 4 |
| \(H_3\) | 2 | 3 | 5 |
| \(H_4\) | 5 | 4 | 2 |
| \(H_5\) | 4 | 6 | 3 |
| \(H_6\) | 7 | 5 | 6 |
| \(H_7\) | 6 | 7 | 7 |
扫描 \(H_7\) 发现所有关系都已经满足。
至此 \(T\) 的空白位置都已经填满,没有新的陪集可以发现,数独游戏结束,这时得到的 \(T\) 就是 \(G/H\) 的最终乘法表。
由此利用宽度优先搜索不难得出陪集间的关系为: \[\begin{array}{l}H_0 = H_0\cdot e,\\ H_1=H_0\cdot\rho_0,\\H_2=H_1\cdot\rho_1=H_0\cdot\rho_0\rho_1,\\H_3=H_2\cdot\rho_0=H_0\cdot\rho_0\rho_1\rho_0,\\ H_4=H_2\cdot\rho_2=H_0\cdot\rho_0\rho_1\rho_2,\\ H_5=H_3\cdot\rho_2=H_0\cdot \rho_0\rho_1\rho_0\rho_2,\\ H_6=H_5\cdot\rho_1=H_0\cdot \rho_0\rho_1\rho_0\rho_2\rho_1,\\ H_7=H_6\cdot\rho_0=H_0\cdot \rho_0\rho_1\rho_0\rho_2\rho_1\rho_0.\end{array}\]
从而其一组陪集代表元可以选为 \[\begin{array}{llll}e&\rho_{0}&\rho_{0}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\\\rho_{0}\rho_{1}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\end{array}\]
这正是我们前面看到过的。
注: 这个例子看似有点长,但还是一个比较简单的例子,其中并没有出现已知陪集重复的情形(Holt 的书中称之为 coincidence)。这种情形的处理麻烦一些,因为一旦出现重复的陪集,就有可能顺藤摸瓜找到更多重复的陪集。这时就要立刻暂停扫描,流程跳转到处理 coincidence:开辟一个栈来存放已知的 coincidence,每次弹出一对,将它们合并,然后把新发现的 coincidence 压入栈中。
星状多胞体的计算
星状多胞体也可以使用 Wythoff 构造法来生成,但是直接套用上面的方法一般是行不通的,我们需要在生成元中加入额外的生成关系。
这里以 Great dodecahedron 为例来说明:其 Coxeter-Dynkin 图为
于是三面镜子的法向量夹角分别为 \(\pi-2\pi/5, \pi/2, \pi-\pi/5\)。如果我们仍然沿用以前的分析,会得出其对称群的表现为 \[K=\langle\tau_0,\tau_1,\tau_2 \ |\ \tau_0^2=\tau_1^2=\tau_2^2=(\tau_0\tau_1)^5=(\tau_1\tau_2)^5=(\tau_0\tau_2)^2=1\rangle.\]
这是一个无限群,而且顶点的稳定化子的商群也是无限的,所以还想按以前的方法计算就行不通了。
实际上我们只要在生成关系中再加上一条 \((\tau_0\tau_1\tau_2\tau_1)^3=1\) 即可,即对称群的表现为
\[\begin{align*} K = \langle\tau_0,\tau_1,\tau_2 \ |\ &\tau_0^2=\tau_1^2=\tau_2^2=(\tau_0\tau_1)^5=(\tau_1\tau_2)^5=\\&(\tau_0\tau_2)^2=(\tau_0\tau_1\tau_2\tau_1)^3=1\rangle. \end{align*}\]
注意到我使用了字母 \(\tau\) 来表示反射,\(K\) 表示 Great dodecahedron 的对称群,这个记号选择是有意的。这是怎么回事呢?先看视频:
(请忽略左边错误的 Coxeter 图,这个 ui 界面我改不动)
由视频可见,Great dodecahedron 与正二十面体 (icosahedron) 共用相同的顶点,并且看起来 Great dodecahedron 可以通过在 icosahedron 表面挖一些三角形的洞得到。这个结论也可以推广:一般地如果星状多面体的洞是一个有 \(h\) 条边的多边形,则对应的额外生成关系就是 \((\tau_0\tau_1\tau_2\tau_1)^h=1\)。
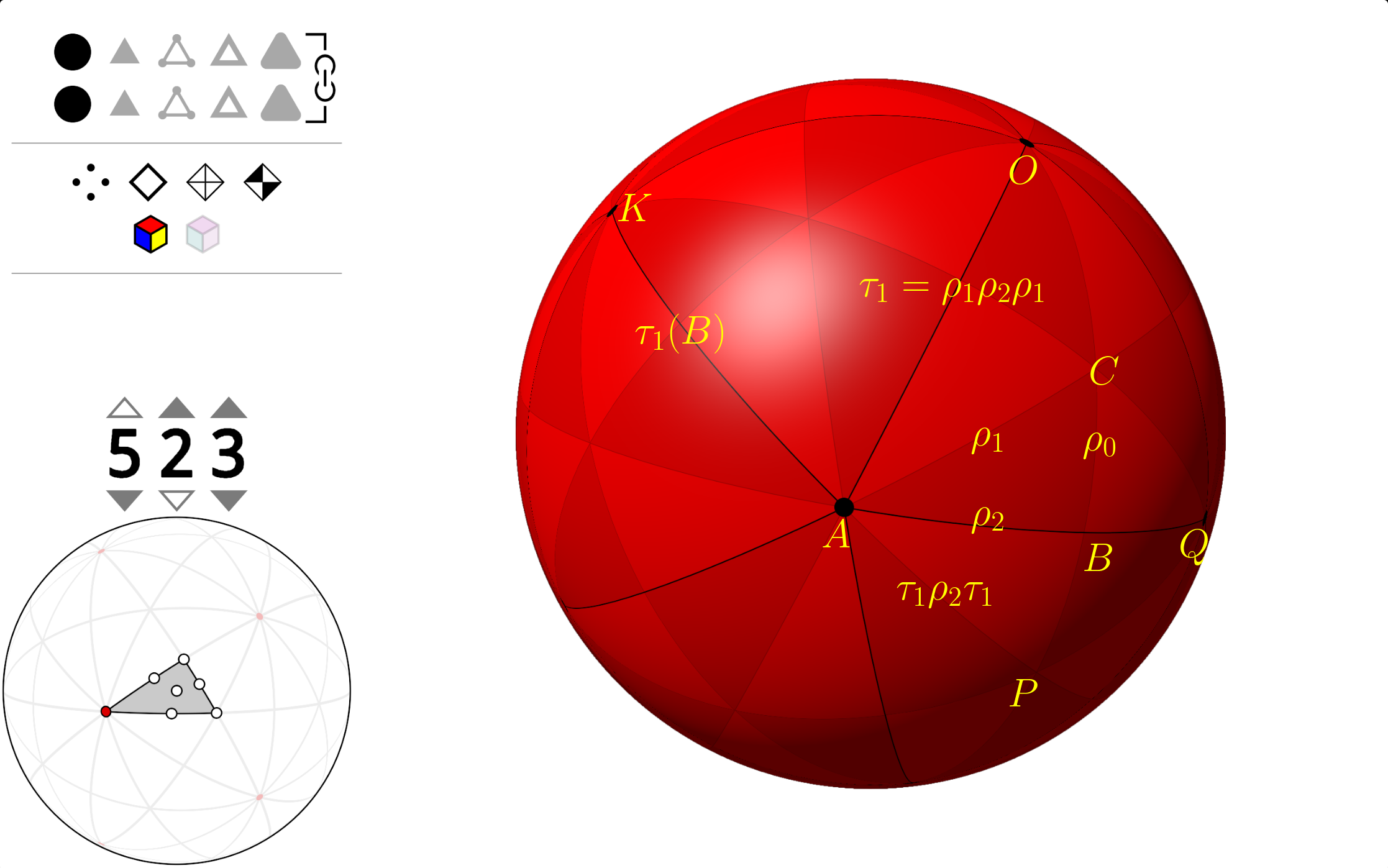
在上图中,\(\Delta ABC\) 是正二十面体的基本区域,三个内角分别是 \(\angle CAB=\pi/5\),\(\angle CBA=\pi/2\),\(\angle ACB=\pi/3\),\(\rho_0,\rho_1,\rho_2\) 分别是关于弧 \(BC, AC, AB\) 的反射。正二十面体的对称群的表现为 \[G = \langle\rho_0,\rho_1,\rho_2\ |\ \rho_0^2=\rho_1^2=\rho_2^2=(\rho_0\rho_1)^3=(\rho_1\rho_2)^5=(\rho_0\rho_2)^2=1\rangle.\]
Great dodecahedron 可以这样得到:沿着正二十面体的边从顶点 \(Q\) 走到 \(A\),右手边的面是三角形 \(\Delta OAQ\),接下来的第一条边应该是 \(AO\),我们跳过这条边,选择第二条边 \(AK\),到达 \(K\) 后继续选择右手边的第二条边,这样绕着 \(O\) 一圈下来共经过 5 条边,它们正好围成 Great dodecahedron 的一个面。对正二十面体的其它边也如此操作会得到 Great dodecahedron 其它的面。
像这样对一个多面体,保持它的顶点和边的集合不变,但是每次选择右手边的第 \(k\) 个边走下去绕一圈获得一个面,这样构造新多面体的方法叫做 Facetting 手术。在我们这个项目中 \(k\) 总是等于 2。
我们来导出正二十面体的对称群 \(G\) 和 Great dodecahedron 的对称群 \(K\) 之间的关系。
来看三角形 \(\Delta OAB\),它的三个内角分别是 \(\angle OAB=2\pi/5\),\(\angle OBA=\pi/2\),\(\angle AOB=\pi/5\),它包含三个与 \(\Delta ABC\) 全等的三角形,关于其三条边 \(OA,OB,AB\) 的反射分别是 \(\tau_1=\rho_1\rho_2\rho_1,\tau_0=\rho_0,\tau_2=\rho_2\) 5。
Facetting 操作 \(\varphi_k\) 用群的语言来描述就是(记住 \(k=2\)) \[G=\langle \rho_0,\rho_1,\rho_2\rangle\xrightarrow{\ \varphi_k\ }\langle\rho_0,\rho_1(\rho_2\rho_1)^{k-1},\rho_2\rangle=\langle\tau_0,\tau_1,\tau_2\rangle=K.\] 一般来说 \(K\) 是 \(G\) 的子群,但在这里 \(G\) 和 \(K\) 就是同一个群。我们不解释为什么 \(G=K\),这里只承认这一点,然后借助这个事实来说明 \(K\) 就是 Great dodecahedron 的对称群。
首先 \(\langle \tau_1,\tau_2\rangle=\langle \rho_1,\rho_2\rangle\) 是顶点 \(A\) 的稳定化子群,所以 Great dodecahedron 和正二十面体的顶点集是一样的。但 \(\tau_1\tau_2\) 是一个角度为 144 度的旋转,这一点和 \(\rho_1\rho_2\) 是一个 72 度的旋转不同,所以 Great dodecahedron 的 vertex configure 是一个五角星,而不像正二十面体那样是一个五边形。
其次 \(\langle\tau_0,\tau_2\rangle=\langle\rho_0,\rho_2\rangle\) 为边 \(AQ\) 的稳定化子群,所以 Great dodecahedron 的边集和正二十面体也是一样的。
它俩的区别在于边组成面的方式不一样。\(\langle\tau_0,\tau_1\rangle\) 是 Great dodecahedron 面的稳定化子群,注意到 \(\tau_1\) 是关于 \(AO\) 的反射,它会把 \(AQ\) 映射为 \(AK\),这正对应选择第 \(k\) 条边的操作。\(\tau_0\tau_1\) 是一个绕着顶点 \(O\) 的角度为 \(2\pi/5\) 的旋转,所以 \(AQ\) 在子群 \(\langle \tau_0,\tau_1\rangle\) 作用下会绕 \(O\) 转一圈,正对应 Facetting 操作得到的一个面。
我们来找出 \(\tau_0,\tau_1,\tau_2\) 之间隐藏的一条生成关系:
注意到 \(\tau_1\tau_2\tau_1=\tau_1\rho_2\tau_1\) 是关于 \(AP\) 的反射,它和 \(\tau_0=\rho_0\) 的复合是绕着 \(P\) 点角度为 \(2\pi/3\) 的旋转,所以 \((\tau_0\tau_1\tau_2\tau_1)^3=1\)。加入这个额外的生成关系得到的就是 \(K\) 的正确的表现: \[\begin{align*} K = \langle\tau_0,\tau_1,\tau_2 \ |\ &\tau_0^2=\tau_1^2=\tau_2^2=(\tau_0\tau_1)^5=(\tau_1\tau_2)^5=\\&(\tau_0\tau_2)^2=(\tau_0\tau_1\tau_2\tau_1)^3=1\rangle. \end{align*}\]
所以我们就可以对 \(K\) 照搬之前的绘制步骤了。
这个额外的生成关系其实也有背后的解释:对 Faceting 手术得到的新多面体再进行一次 Faceting 手术是可以回到原来的多面体的。对 great dodecahedron 每次沿着它的边,选择当前离开的边的右手第二个边走下去,即从 \(Q\) 走到 \(A\) 时,不是选择 \(AK\) 继续走下去,而是选择 \(AO\),这样走下去又会得到正二十面体的三角形的面,这对应的就是额外的生成关系中的指数 3。
这一点从群上也可以得到验证。
\[K=\langle \tau_0,\tau_1,\tau_2\rangle\xrightarrow{\ \varphi_2\ }\langle\tau_0,\tau_1\tau_2\tau_1,\tau_2\rangle=\langle\rho_0,\rho_2\rho_1\rho_2,\rho_2\rangle=G.\]
关于 Faceting 手术可以在 McMullen 和 Schulte 所著的 Abstract Regular Polytopes 一书中找到。
Snub cube 的计算
如果你理解了上面的内容,snub 多面体的情形也是不难理解的。我以 snub cube 来说明:
Snub cube 和 cube 的区别在于它的对称群只包含旋转,我们已经看到 cube 的对称群 \(G\) 的表现为 \[G = \langle\rho_0,\rho_1,\rho_2\ |\ \rho_0^2=\rho_1^2=\rho_2^2=(\rho_0\rho_1)^4=(\rho_1\rho_2)^3=(\rho_0\rho_2)^2=1\rangle.\] 它有 48 个元素,其中 24 个是旋转。这些旋转可以由 \(r_0=\rho_0\rho_1, r_1=\rho_1\rho_2,r_2=\rho_0\rho_2\) 生成 (由于 \(r_0r_1=r_2\) 因此实际上可以由 \(r_0\) 和 \(r_1\) 生成)。这 24 个旋转就构成了 Snub cube 的对称群 \(\widetilde{G}\)。
不难写出 \(\widetilde{G}\) 的表现为 \[\widetilde{G}=\langle r_0,r_1\ |\ r_0^4=r_1^3=(r_0r_1)^2=1\rangle.\]
利用 Todd-Coxeter 算法不难求出这个群的所有 24 个元素:
\[\begin{array}{lll}e&r_{0}&r_{0}r_{0}\\r_{0}r_{0}r_{0}&r_{1}&r_{1}r_{1}\\r_{0}r_{1}&r_{0}r_{1}r_{1}&r_{0}r_{0}r_{1}\\r_{0}r_{0}r_{1}r_{1}&r_{0}r_{0}r_{0}r_{1}&r_{1}r_{0}\\r_{1}r_{0}r_{0}&r_{1}r_{0}r_{0}r_{0}&r_{1}r_{1}r_{0}\\r_{1}r_{1}r_{0}r_{0}&r_{0}r_{1}r_{1}r_{0}&r_{0}r_{1}r_{1}r_{0}r_{0}\\r_{0}r_{0}r_{1}r_{1}r_{0}&r_{1}r_{0}r_{0}r_{1}&r_{1}r_{0}r_{0}r_{1}r_{1}\\r_{1}r_{0}r_{0}r_{0}r_{1}&r_{1}r_{1}r_{0}r_{0}r_{1}&r_{0}r_{1}r_{1}r_{0}r_{0}r_{1}\end{array} \]
注意在 snub 的情形初始顶点 \(v_0\) 不属于任何镜面,所以其稳定化子群只有单位元 1,即每个 \(g\in\widetilde{G}\) 把 \(v_0\) 变换为不同的顶点。将它们作用在 \(v_0\) 上即得 snub cube 的所有顶点。
我们现在利用轨道—稳定化子的理论来求 snub cube 的边。snub cube 的边也是分类型的,每个 \(r_i(i=0,1,2)\) 作用在 \(v_0\) 上可得一个类型为 \(i\) 的边 \(e_i=(v_0, v_0\cdot r_i)\) 6,我们来定出 \(e_i\) 的稳定化子群 \(H\)。
首先注意到任何 \(g\in G\) 如果保持 \(e_i\) 不变,则只有两种可能,要么它保持 \(e_i\) 上每个点不变,要么它将 \(e_i\) 关于其中点进行翻转。这一点对 \(g\in\widetilde{G}\) 自然也成立。所以若 \(g\in\widetilde{G}\) 保持 \(e_i\) 不变,则要么 \(v_0g = v_0, v_0r_i=v_0r_ig\),要么 \(v_0g = v_0r_i,v_0r_ig=v_0\)。前一种情形说明 \(g\) 属于 \(v_0\) 的稳定化子群从而只能是单位元;后一种情形说明 \(r_ig\) 和 \(r_ig^{-1}\) 都属于 \(v_0\) 的稳定化子群从而 \(r_ig=r_ig^{-1}=1\),即 \(g=r_i\) 且 \(r_i^2=1\)。总之我们证明了只有在 \(r_i^2=1\) 时 \(e_i\) 才有非平凡的稳定化子群,这时稳定化子群是二阶循环群 \(\langle r_i\rangle\)。
于是 snub cube 的类型为 \(r_0\) 和 \(r_1\) 的边的个数都是 24/1=24 个;类型为 \(r_2\) 的边的个数为 24/2=12 个,从而 snub cube 总共有 24+24+12=60 条边。
snub cube 的面可以这样求:由于 \(r_0^4=1\) 所以 \(r_0\) 可以生成一个正四边形的面,类似地由于 \(r_1^3=1\) 所以 \(r_1\) 可以生成一个正三角形的面,而由于 \(r_2^2=1\) 所以 \(r_2\) 生成的面是退化的。这种由单个旋转生成的面的稳定化子群是很好求的:若 \(g\) 保持 \(r_i\) 生成的面不变,则其必然把某个形如 \(v_0r_i^k\) 的顶点变换为 \(v_0\),即 \(g=r_i^{-k}\) 是 \(r_i\) 的某次幂,反之易见 \(r_i\) 的任何幂都保持此面不变,所以其稳定化子群即为循环群 \(\langle r_i\rangle\)。
于是 \(r_0\) 生成的面的个数为 24/4=6,\(r_1\) 生成的面的个数为 24/3=8,\(r_2\) 生成的面都退化因而个数是 0,总计 14 个面。
小心!我们还漏掉了一种三角面,它源自 \(r_0r_1=r_2\) 这个关系。考虑 \(\{v_0, v_0r_1, v_0r_2\}\) 这三个顶点,这三个顶点中 \((v_0,v_0r_1)\) 构成一条类型为 \(r_1\) 的边, \((v_0,v_0r_2)\) 构成一条类型为 \(r_2\) 的边,而 \(r_0r_1=r_2\) 这个关系告诉我们 \[(v_0, v_0r_0)\xrightarrow{\ r_1\ }(v_0r_1, v_0r_0r_1) = (v_0r_1, v_0r_2).\] 即 \((v_0r_1, v_0r_2)\) 是一条类型为 \(r_0\) 的边,它是由将 \(r_1\) 作用在类型为 \(r_0\) 的初始边 \((v_0, v_0r_0)\) 上得到的,于是 \(\{v_0, v_0r_1, v_0r_2\}\) 构成一个三角形的三个顶点,其三条边在对称群作用下属于不同的轨道,所以这个三角形的稳定化子必然保持每条边不变,从而只能是恒等元,从而这样的面有 24/1=24 个。
于是 snub cube 一共有 14+24=38 个不同的面。
这里介绍的方法也适用于其它的 snub 多面体以及 snub 24-cell。
多面体的顶点投影到 Coxeter 平面
项目中还实现了一个
draw_on_coxeter_plane(*args, **kwargs)
方法,用于绘制将多面体的顶点投影到其 Coxeter
平面上后得到的图案,例如下图显示的是将 600-cell 的 120 个顶点投影到其
Coxeter 平面上的结果:
你可以和 wikipedia 上的效果 比较一下。
附录:手算 Todd-Coxeter
对简单的群,Todd-Coxeter 算法完全可以用手算快速得出结果。我非常推荐 Borcherds 的视频,他的演示非常精彩:
仿照 Borcherds 的方法,前面正方形的例子可以很快写出来:
我来解释一下步骤:我们将画出一个有限图,图的每个顶点代表 \(H=\langle s_0,s_1\rangle\) 的一个陪集,每个顶点有三条不同颜色的边,表示此陪集在生成元 \(s_i\) 作用下的结果。
- 首先我们在空白纸上画出第一个顶点,它对应的陪集是 \(H=H_0\) 自身。\(H\) 包含 \(s_0,s_1\),所以红、绿边是自边。\(s_2\),即蓝色的边,会把它映射为一个新顶点 \(H_1\)。
- 从 \(H_0\) 出发,利用红蓝交换,可得红色保持 \(H_1\) 不动。但是绿蓝不交换,所以绿色将 \(H_1\) 映射为新顶点 \(H_2\)。
- \((\text{绿蓝})^3=1\),即 \(H_2\xrightarrow{(\text{绿蓝})^3}H_2\),所以 \[H_2\xrightarrow{\text{绿}} H_1\xrightarrow{\text{蓝}} H_0\xrightarrow{\text{绿}} H_0\xrightarrow{\text{蓝}} H_1\xrightarrow{\text{绿}} H_2\xrightarrow{\text{蓝}} H_2.\] 所以蓝色保持 \(H_2\) 不动。红绿不交换,所以红色将 \(H_2\) 映射为新顶点 \(H_3\)。
- 仿照上面的分析继续下去,可以发现到 \(H_5\) 时,三种颜色的边不会给出新顶点。所以 \(\{H_0,\ldots,H_5\}\) 就是 \(G/H\) 的全部陪集。



