Coxeter 群,有限状态机与均匀密铺
更新:由于使用 POV-Ray 渲染三维双曲蜂巢非常的慢,所以我放弃了这种途径,并将代码从 Github 主分支中移除。你可以在 旧存档 中找到本文使用的代码。关于怎样渲染双曲蜂巢读者可以参考 另一个项目。
本文介绍我刚刚完成的一个 Python 程序。虽然是刚刚完成,但是它占去了我这半年来大部分的业余时间,也算是一个艰苦攻关,呕心沥血之作。主要是它涉及的理论比较复杂,要用到 Coxeter 群的一些深刻的性质,即所谓的 automatic property。这半年里面不少时间是花在学习 Casselman 和 Brink & Howlett 等人的文章上面,这才弄懂了其中的数学原理(见参考文献)。
虽然完成这个程序很有成就感,但是我无意强调这个程序的任何优越性:它采用的 Coxeter 群的计算方法并不先进,难入行家的法眼。而且它的代码比较丑,大概率除了我,别人也很难用起来。
这个程序的目的是使用群论的方式来绘制二维和三维的各种 均匀密铺。所谓均匀密铺,你可以理解为用一些正多边形的瓷砖密铺整个空间,使得瓷砖的顶点在对称群作用下是传递的(构成单一轨道)。
我先展示一些这个程序的例子,然后介绍它的实现原理。
例子
以下图片均由此程序绘制:
Euclidean 密铺 omnitruncated (4, 2, 4):

二维 Poincaré 圆盘上的正双曲密铺 (2, 3, 13),绘制了 3447 个顶点,6971 条边,3549 个多边形:

二维上半平面模型中的双曲密铺 omnitruncated (4, 3, 3):

三维 Poincaré 单位球中的正双曲密铺 (3, 5, 3):

三维 Poincaré 单位球中的正双曲密铺 (5, 3, 5):

三维 Poincaré 单位球中的正双曲密铺 (5, 3, 4):

三维 Poincaré 单位球中的正双曲密铺 (4, 3, 5):

以上四个密铺是三维双曲空间中仅有的正且每个胞腔为紧集的双曲密铺。如果去掉每个胞腔为紧集的限制的话,但是要求每个胞腔的体积有限的话,则还有 10 个正双曲密铺,如下图的 (6, 3, 3):

你可以看到每个胞腔都有一个理想顶点,它位于空间的无穷远处 (即单位球面上)。这种密铺叫做仿紧的 (paracompact),因为每个胞腔的体积仍然是有限的。如果再去掉每个胞腔的体积有限的条件的话,得到的密铺叫做非紧的,非紧的密铺有无限多个。
如果去掉正密铺这个限制,只考虑均匀密铺的话,那例子就非常多了。比如我们可以从正密铺出发通过截断操作得到许多均匀密铺,如 rectified (3, 5, 3) 和 rectified (5, 3, 4):


二维的球面密铺 omnitruncated (5, 2, 3):

最后是一个 shader 程序,来自 Matt Zucker 的 shadertoy 项目:
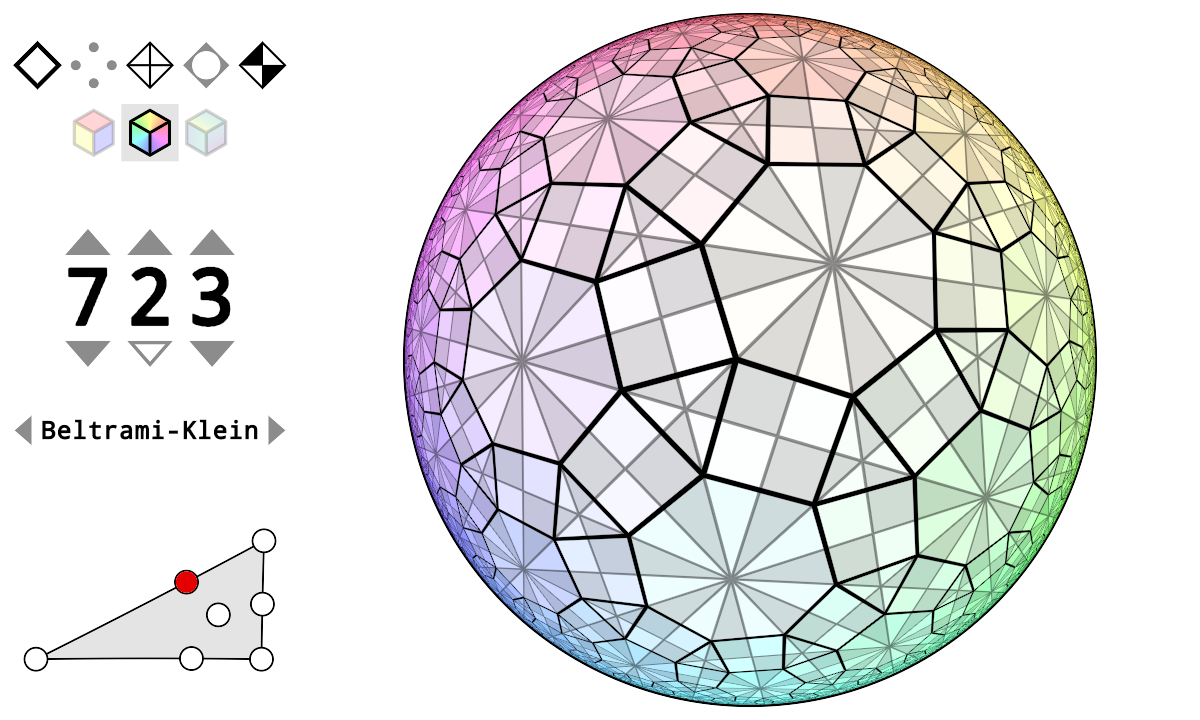
Wythoff 构造法
绘制均匀密铺的理论基础是所谓的 Wythoff 构造法,也叫万花筒方法。即在空间中摆放若干反射平面 (镜子),然后从一个初始点出发,关于这些镜子反复作反射变换,得到所有的虚像,就得到了密铺的全部顶点。
下面的视频演示了 Wythoff 构造法的效果:在二维的 Poincaré 双曲圆盘中,房间四周的墙壁都是镜子,房间中的场景在镜子中反复成像,得到了无数个虚像房间,它们填满了整个双曲空间。但实际上这个场景里面只有观察者所在的房间是真实的,其它房间都是它在镜子中的虚像。
在编程实现 Wythoff 构造法时有两种不同的方案:
逆像素方法。这种方法是对图像中的每个像素,计算它在空间中的对应点 \(p\),然后将 \(p\) 反复作镜面反射,直到其落入基本区域为止,得到一个点 \(q\)。即我们找到 \(p\) 在房间中的原像 \(q\)。然后根据 \(q\) 在基本区域中的位置给 \(p\) 对应的像素上色。这种方法可以对所有像素并行计算,特别是和 shader 编程结合起来可以生成非常惊艳的效果。这里举两个 shadertoy 上的例子:
逆像素方法只关心像素的颜色,完全不关心它的坐标是什么。它输出的是光栅图,无法输出矢量图形。而且如果你想导出数据用在建模软件中的话也不太方便。
坐标方法。这种方法就是从给定初始点 \(v_0\) 出发,计算它的所有虚像(限定顶点数目的阈值),以及边和面的连接关系,然后逐个进行绘制。这种方法可以获取顶点具体的坐标信息,并输出为矢量图形和模型文件,比较适合用在学术论文中。但是它无法并行,而且对双曲密铺这种指数增长的结构计算效率是很慢的。
我的这个程序采用的是坐标方法。它首先在密铺的对称群中进行符号计算,得出每个顶点在最短字典序下对应的单词表示。(一个单词就是一个元素都是整数的
tuple),以及边和面的连接关系(也是元素都是整数的
tuple),然后将每个顶点对应的单词作用在初始顶点上得到该顶点的浮点坐标。换句话说,在计算每个顶点的最终坐标之前,它已经提前计算好了有多少个顶点,每个顶点是由初始顶点经过哪些反射得到的,哪些顶点构成边,哪些顶点构成面,哪些顶点构成胞腔,等等。这些计算仅涉及整数运算,完全避免了浮点数精度损失的问题。
听起来很神奇?下面我用一个例子来演示具体的步骤。
例子:omnitruncated (7, 2, 3) 密铺
Omnitruncated (7, 2, 3) 密铺对应的 Coxeter-Dynkin 图如下:
这是一个二维的双曲密铺,其对称群是由 Coxeter 矩阵
\[M=\begin{pmatrix} 1 & 7 & 2 \\ 7 &1 &3\\ 2 & 3 &1\end{pmatrix}\]
给出的 Coxeter 群
\[W=\langle s_0,s_1, s_2\ |\ s_0^2=s_1^2=s_2^2=(s_0s_1)^7=(s_1s_2)^3=(s_0s_2)^2=1\rangle.\]
初始顶点不包含于任何镜面上,所以其稳定化子群只包含单位元 1,从而根据 轨道—稳定化子定理 \(W\) 的每一个元素都对应密铺中的一个顶点。
\(W\) 中每个元素 \(w\) 都可以表示为生成元 \(s_0,s_1,s_2\) 的乘积,我们称任何这样的表示方式为 \(w\) 的一个单词表示。如果 \(w=s_{i_1}s_{i_2}\cdots s_{i_k}\) 是一个单词表示,且 \(w\) 不存在长度小于 \(k\) 的表示,我们就称 \(s_{i_1}s_{i_2}\cdots s_{i_k}\) 是 \(w\) 的一个既约表示,并称 \(l(w)=k\) 是 \(w\) 的长度。
\(w\) 的既约表示一般不是唯一的,比如从 \(W\) 的生成关系中可以看出 \(s_0s_2=s_2s_0\), \(s_1s_2s_1=s_2s_1s_2\) 等等。但是 \(w\) 的所有既约表示的长度必然都是一样的,所以 \(l(w)\) 的定义合理。
我们可以给 \(w\) 的所有既约表示排序,并选择最小的那个来作为 \(w\) 的规范表示。这个排序的依据叫做最短字典序 (shortlex order)。最短字典序顾名思义,就是字典在排列单词时采用的次序。
首先规定生成元 \(s_0,s_1,s_2\) 之间的字母顺序关系为 \(s_0<s_1<s_2\),然后将这个顺序扩展到任何两个既约表示 \(w_1\) 和 \(w_2\) 上去:
最短字典序. 设 \(w_1=s_{i_1}s_{i_2}\cdots s_{i_n}\) 和 \(w_2=s_{j_1}s_{j_2}\cdots s_{j_m}\) 是两个不同的既约表示,\(w_1,w_2\) 可以是不同的群元素。它们二者在最短字典序中的关系由如下方式确定:
- 先比较长度,长度不同的话,长度小的为较小者,即若 \(n<m\) 则 \(w_1<w_2\),反之若 \(n>m\) 则 \(w_1>w_2\)。
- 若长度相等则按字母顺序从左到右逐项比较,设 \(k\) 使得对任何 \(l<k\) 有 \(s_{i_l}=s_{j_l}\) 但 \(s_{i_k}\ne s_{j_k}\),则规定 \(w_1,w_2\) 之间的大小关系与 \(s_{i_k},s_{j_k}\) 之间的大小关系相同。
于是任何 \(w\in W\) 在最短字典序下都有唯一的规范表示。
定义 \(\mathcal{SL}(W)\) 为 \(W\) 中所有元素的规范表示组成的集合,下面列出了 \(\mathcal{SL}(W)\) 中所有长度不超过 5 的元素,一共有 37 个:(从小到大按行排列)
\[ \begin{array}{lllll}e&s_{0}&s_{1}&s_{2}&s_{0}s_{1}\\s_{0}s_{2}&s_{1}s_{0}&s_{1}s_{2}&s_{2}s_{1}&s_{0}s_{1}s_{0}\\s_{0}s_{1}s_{2}&s_{0}s_{2}s_{1}&s_{1}s_{0}s_{1}&s_{1}s_{0}s_{2}&s_{1}s_{2}s_{1}\\s_{2}s_{1}s_{0}&s_{0}s_{1}s_{0}s_{1}&s_{0}s_{1}s_{0}s_{2}&s_{0}s_{1}s_{2}s_{1}&s_{0}s_{2}s_{1}s_{0}\\s_{1}s_{0}s_{1}s_{0}&s_{1}s_{0}s_{1}s_{2}&s_{1}s_{0}s_{2}s_{1}&s_{1}s_{2}s_{1}s_{0}&s_{2}s_{1}s_{0}s_{1}\\s_{0}s_{1}s_{0}s_{1}s_{0}&s_{0}s_{1}s_{0}s_{1}s_{2}&s_{0}s_{1}s_{0}s_{2}s_{1}&s_{0}s_{1}s_{2}s_{1}s_{0}&s_{0}s_{2}s_{1}s_{0}s_{1}\\s_{1}s_{0}s_{1}s_{0}s_{1}&s_{1}s_{0}s_{1}s_{0}s_{2}&s_{1}s_{0}s_{1}s_{2}s_{1}&s_{1}s_{0}s_{2}s_{1}s_{0}&s_{1}s_{2}s_{1}s_{0}s_{1}\\s_{2}s_{1}s_{0}s_{1}s_{0}&s_{2}s_{1}s_{0}s_{1}s_{2}&\end{array} \]
理论上由 \(s_0,s_1,s_2\) 组成的所有可能的长度不超过 5 的单词总共有 \(\sum_{i=0}^5 3^i=364\) 个,上表告诉我们实际上它们只包含了 \(W\) 中 37 个不同的元素,即将它们作用在密铺中的初始顶点上只会得到 37 个顶点,其余 364 - 37 = 327 个都是重复的。进一步计算可得长度不超过 6 的单词有 1093 个而实际上只包含了 53 个不同的元素。所以如果我们能够快速地生成 \(\mathcal{SL}(W)\) 中的元素而不是去遍历所有可能单词的话,就可以大大提高计算效率。
那么怎么计算 \(\mathcal{SL}(W)\) 中的元素呢?这就引出了一个关于 Coxeter 群的重要结论:
[Brigitte Brink & Robert B. Howlett, 1993]. 若 \(W\) 是有限生成 Coxeter 群,则 \(\mathcal{SL}(W)\) 是一个 正则语言。
正则语言这个术语来自计算机科学,关于正则语言的一个基本事实是,一个有限字符集上的正则语言总是可以被一个确定的有限状态自动机 (definite finite automaton) 识别,这样的有限状态机不是唯一的,但是在等价意义下(对状态重新标号)总是存在一个状态数目最少的。下图显示的是识别 (7, 2, 3) 这个群的 \(\mathcal{SL}(W)\) 的最小状态机:
可以看到在上图中一共有 19 个节点 (即状态),每个状态都有一个编号,这个编号并没有实际意义,可以不用理会,实际上给状态重新编号不影响有限状态机识别的语言。真正有意义的是顶点之间的关系以及边的编号。圈红的节点 0 是初始状态。
图中的每条有向边规定了状态之间的转移规则,边的标号 \(i\) 代表生成元 \(s_i\)。从初始状态出发,每次沿着一条有向边移动到下一个状态,经过的路径给出了一个由 \(s_0,s_1,s_2\) 组成的单词,所有的路径给出的单词组成的集合就是这个有限状态机识别的语言,即 \(\mathcal{SL}(W)\)。
举个例子:
- 长度为 0 的路径对应的是 \(W\) 的单位元。
- 长度为 1 的三条路径 \[\begin{align*}0&\xrightarrow{\ s_0\ }1,\\ 0&\xrightarrow{\ s_1\ }2,\\ 0&\xrightarrow{\ s_2\ }8.\end{align*} \] 对应的是 \(W\) 的三个长度为 1 的元素 \(s_0,s_1,s_2\)。
- 长度为 2 的 5 条路径 \[\begin{align*}0&\xrightarrow{\ s_0\ }1\xrightarrow{\ s_1\ }2\\ 0&\xrightarrow{\ s_0\ }1\xrightarrow{\ s_2\ }8\\ 0&\xrightarrow{\ s_1\ }2\xrightarrow{\ s_0\ }3\\ 0&\xrightarrow{\ s_1\ }2\xrightarrow{\ s_2\ }8\\ 0&\xrightarrow{\ s_2\ }8\xrightarrow{\ s_1\ }9\end{align*} \] 对应的是 \(W\) 的 5 个长度为 2 的元素 \(s_0s_1,s_0s_2,s_1s_0,s_1s_2,s_2s_1\)。
以此类推,我们可以很容易用宽度优先搜索来不重复不遗漏地遍历任意长度范围内的群元素。特别地如果你按图索骥地验证一下的话可以发现所有长度不超过 5 的路径一共有 37 条,它们正对应前面列出的 \(\mathcal{SL}(W)\) 中长度不超过 5 的 37 个单词。
无限 Coxeter 群的有限状态机必然含有回路,而有限 Coxeter 群的有限状态机则必然是一个以初始状态为根节点的有向树。例如下图显示的是置换群 \(S_4\) 对应的有限状态机:
用宽度优先搜索可以得出其包含 24 条不同的路径,它们对应 \(S_4\) 的 24 个元素的最短字典序表示:
\[ \begin{array}{llll}e&s_{0}&s_{1}&s_{2}\\s_{0}s_{1}&s_{0}s_{2}&s_{1}s_{0}&s_{1}s_{2}\\s_{2}s_{1}&s_{0}s_{1}s_{0}&s_{0}s_{1}s_{2}&s_{0}s_{2}s_{1}\\s_{1}s_{0}s_{2}&s_{1}s_{2}s_{1}&s_{2}s_{1}s_{0}&s_{0}s_{1}s_{0}s_{2}\\s_{0}s_{1}s_{2}s_{1}&s_{0}s_{2}s_{1}s_{0}&s_{1}s_{0}s_{2}s_{1}&s_{1}s_{2}s_{1}s_{0}\\s_{0}s_{1}s_{0}s_{2}s_{1}&s_{0}s_{1}s_{2}s_{1}s_{0}&s_{1}s_{0}s_{2}s_{1}s_{0}&s_{0}s_{1}s_{0}s_{2}s_{1}s_{0}\end{array} \]
既然通过 \(\mathcal{SL}(W)\) 来生成群元素如此方便,那问题来了:
问题 3.1: 怎样计算 \(\mathcal{SL}(W)\) 对应的有限状态机?
此问题技术太过复杂,完整介绍全部内容的话本文难以承受,我在后面的附录中作了一些简单的解释。
有了每个群元素的唯一的规范表示,我们就可以很容易地计算密铺中每个顶点的坐标了:
设 \(w=s_{i_0}s_{i_1}\cdots s_{i_n}\),初始顶点为 \(v_0\),则 \(w\) 在 \(v_0\) 上的作用为 \[w\cdot v_0 = s_{i_0}(s_{i_1}(\cdots s_{i_n}(v_0))).\] 即从右到左依次计算每个生成元作用的结果。当然由于 \(W\) 是无限群,我们只能计算那些长度不超过一定范围的群元素对应的顶点。假设我们已经有了前面这 37 个顶点,它们存储在一个列表 \(L\) 里。为了绘制密铺中的边,我们还需要计算 \(L\) 中哪些顶点是相邻的,这个怎么解决呢?
首先我们需要计算一个 \(L\)
中元素之间的乘法表 \(T\),\(T\)
的作用是帮助我们查找任何一个单词,其规范表示在 \(L\) 中的下标 (不在 \(L\) 中的话则返回 None)。\(T\) 是一个大小为 \(|L|\times 3\) 的二维数组,其第 \(i\) 行对应 \(L\) 中的第 \(i\) 个群元素 \(w_i\),第 \(j\) 列对应群的生成元 \(s_j\),\(T[i][j]\) 的值等于 \(s_jw_i\) 这个元素的规范表示在 \(L\) 中的下标。如果这个元素不在 \(L\) 中则以 None 代替。
在我们的例子中 \(T\) 的值如下,\(L\) 中的元素放在了第二列:
点击展开列表 \(T\)
| V | word | \(s_0\) | \(s_1\) | \(s_2\) |
|---|---|---|---|---|
| 0 | \(e\) | 1 | 2 | 3 |
| 1 | \(s_{0}\) | 0 | 6 | 5 |
| 2 | \(s_{1}\) | 4 | 0 | 8 |
| 3 | \(s_{2}\) | 5 | 7 | 0 |
| 4 | \(s_{0}s_{1}\) | 2 | 12 | 11 |
| 5 | \(s_{0}s_{2}\) | 3 | 13 | 1 |
| 6 | \(s_{1}s_{0}\) | 9 | 1 | 15 |
| 7 | \(s_{1}s_{2}\) | 10 | 3 | 14 |
| 8 | \(s_{2}s_{1}\) | 11 | 14 | 2 |
| 9 | \(s_{0}s_{1}s_{0}\) | 6 | 20 | 19 |
| 10 | \(s_{0}s_{1}s_{2}\) | 7 | 21 | 18 |
| 11 | \(s_{0}s_{2}s_{1}\) | 8 | 22 | 4 |
| 12 | \(s_{1}s_{0}s_{1}\) | 16 | 4 | 24 |
| 13 | \(s_{1}s_{0}s_{2}\) | 17 | 5 | 23 |
| 14 | \(s_{1}s_{2}s_{1}\) | 18 | 8 | 7 |
| 15 | \(s_{2}s_{1}s_{0}\) | 19 | 23 | 6 |
| 16 | \(s_{0}s_{1}s_{0}s_{1}\) | 12 | 30 | 29 |
| 17 | \(s_{0}s_{1}s_{0}s_{2}\) | 13 | 31 | 28 |
| 18 | \(s_{0}s_{1}s_{2}s_{1}\) | 14 | 32 | 10 |
| 19 | \(s_{0}s_{2}s_{1}s_{0}\) | 15 | 33 | 9 |
| 20 | \(s_{1}s_{0}s_{1}s_{0}\) | 25 | 9 | 35 |
| 21 | \(s_{1}s_{0}s_{1}s_{2}\) | 26 | 10 | 36 |
| 22 | \(s_{1}s_{0}s_{2}s_{1}\) | 27 | 11 | 34 |
| 23 | \(s_{1}s_{2}s_{1}s_{0}\) | 28 | 15 | 13 |
| 24 | \(s_{2}s_{1}s_{0}s_{1}\) | 29 | 34 | 12 |
| 25 | \(s_{0}s_{1}s_{0}s_{1}s_{0}\) | 20 | None | None |
| 26 | \(s_{0}s_{1}s_{0}s_{1}s_{2}\) | 21 | None | None |
| 27 | \(s_{0}s_{1}s_{0}s_{2}s_{1}\) | 22 | None | None |
| 28 | \(s_{0}s_{1}s_{2}s_{1}s_{0}\) | 23 | None | 17 |
| 29 | \(s_{0}s_{2}s_{1}s_{0}s_{1}\) | 24 | None | 16 |
| 30 | \(s_{1}s_{0}s_{1}s_{0}s_{1}\) | None | 16 | None |
| 31 | \(s_{1}s_{0}s_{1}s_{0}s_{2}\) | None | 17 | None |
| 32 | \(s_{1}s_{0}s_{1}s_{2}s_{1}\) | None | 18 | None |
| 33 | \(s_{1}s_{0}s_{2}s_{1}s_{0}\) | None | 19 | None |
| 34 | \(s_{1}s_{2}s_{1}s_{0}s_{1}\) | None | 24 | 22 |
| 35 | \(s_{2}s_{1}s_{0}s_{1}s_{0}\) | None | None | 20 |
| 36 | \(s_{2}s_{1}s_{0}s_{1}s_{2}\) | None | None | 21 |
于是对任意的单词 \(w=s_{i_0}s_{i_1}\cdots
s_{i_n}\),我们可以从 \(T\) 的第
0 行出发,先找到 \(s_{i_n}\) 在 \(L\) 中对应的元素,假设是第 \(k\) 个,那么就跳到第 \(k\) 行,由 \(s_{i_{n-1}}\) 对应的列找到 \(s_{i_{n-1}}s_{i_n}\) 在 \(L\) 中对应的元素,再顺藤摸瓜找到 \(s_{i_{n-2}}s_{i_{n-1}}s_{i_n}\) 在 \(L\) 中对应的元素,…,如此下去即可确定 \(w\) 在 \(L\) 中对应的元素 (或者
None)。
有了表 \(T\) 的帮助,我们可以来计算边的信息了。这里一条边 \(e\) 用一对整数 \(e=(i,j)\) 来表示,\(i,j\) 分别是 \(e\) 的两个端点在 \(L\) 中的下标。
假设初始顶点 \(v_0\) 关于第 \(i\) 面镜子反射后得到的虚像是 \(v_1=s_i(v_0)\),则 \(e=(v_0,v_1)\) 构成一条类型为 \(i\) 的边。在我们这个情形下,边 \(e\) 的稳定化子群是标准椭圆子群 \(W_I=\langle
s_i\rangle\)。根据轨道—稳定化子定理,密铺中所有类型为 \(i\) 的边可以通过将商群 \(W/W_I\) 的每个元素作用在 \(e\) 上得到。显然 \(e\) 的两个端点对应的规范表示分别是单位元 1
和 \(s_i\)。对任一 \(w\in W\),我们首先计算 \(w\) 关于 \(W_I\) 的陪集代表元 \(w_I\),\(w_I\cdot
e\) 的两个端点对应的单词分别是 \(w_I\) 和 \(w_Is_i\),然后按照上面的步骤找到它俩在
\(L\)
中对应的元素下标,这就得到了边对应的下标表示。当然如果出现了
None 说明这条边连接了不在 \(L\) 中的顶点,需要丢掉。
\(L\) 中 37 个顶点构成的边如下:
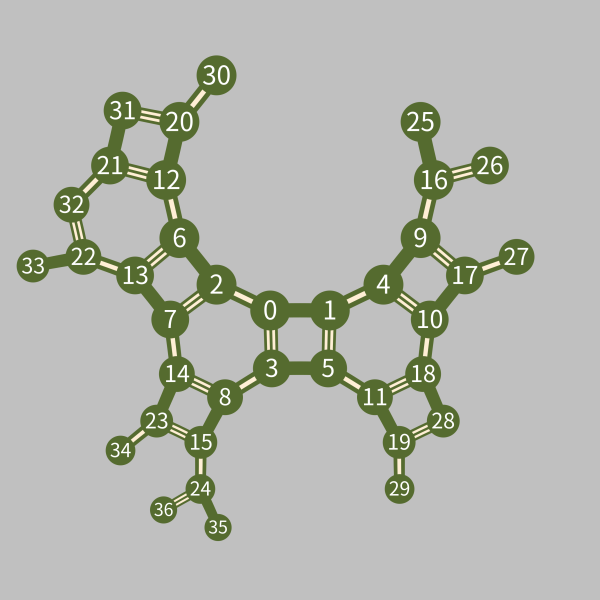
图中标号 0 的顶点是初始顶点,其对应的单词是单位元 1。边中白色的线条个数表示这条边的类型,
从这个图里可以看出很多有用的信息,非常有助于理解 Coxeter 群的最短字典序表示与密铺顶点的对应关系:
- 首先可以看出将顶点 0 关于三个镜面进行一次反射得到的新虚像是 1, 2, 3,它们对应的单词是 \(L\) 中长度为 1 的 \(s_0,s_1,s_2\)。
- 将顶点 0 关于各个镜面进行两次反射得到的新虚像是 4, 5, 6, 7, 8,它们对应的单词是 \(L\) 中长度为 2 的 \(s_0s_1,s_0s_2,s_1s_0,s_1s_2,s_2s_1\)。
- 所有顶点与初始顶点之间的最短路径的长度都不超过 5。
- 一个单词 \(w=s_{i_0}s_{i_1}\cdots s_{i_n}\) 作用在 0 号顶点上 (\(s_{i_n}\) 先作用,\(s_{i_0}\) 在最后) 的结果是一条从 0 号顶点出发,标号依次为 \(s_{i_0}, s_{i_1},\ldots,s_{i_n}\) 的路径 (\(s_{i_0}\) 在先,\(s_{i_n}\) 在最后),与作用的顺序相反。
- 从图中我们可以看出每个顶点对应的单词的规范表示。例如从 0 号顶点到 33 号顶点有两条最短路径:\[ \begin{align*}&0\xrightarrow{\ s_1\ }2\xrightarrow{\ s_0\ }6\xrightarrow{\ s_2\ }13\xrightarrow{\ s_1\ }22\xrightarrow{\ s_0\ }33.\\ &0\xrightarrow{\ s_1\ }2\xrightarrow{\ s_2\ }7\xrightarrow{\ s_0\ }13\xrightarrow{\ s_1\ }22\xrightarrow{\ s_0\ }33. \end{align*}\] 只要按顺序连起来 (从左到右) 就可以得到 33 号顶点对应的两个单词:\(s_1s_0s_2s_1s_0\) 和 \(s_1s_2s_0s_1s_0\),它们都把 0 号顶点变为 33 号顶点,但是前者才是最短字典序表示。这一点也可以从顶点标号中看出来:从 2 号顶点开始两条路径分别去了 6 号和 7 号顶点,由于 6 号顶点对应的单词在 \(\mathcal{SL}(W)\) 中更小,因此这条路径必然才是 33 号顶点规范表示对应的路径。
计算面的步骤也是完全类似的,初始顶点关于 \(i, j\) 两面镜子的反射的复合是一个旋转,这个旋转连续作用 \(m\) 次可以生成一个正多边形的面,其中 \(m\) 是 Coxeter 矩阵中的 \((i,j)\) 分量。这个多边形的稳定化子群是标准椭圆子群 \(W_I=\langle i, j\rangle\),我们仍然可以得出每个顶点对应的一个单词表示,用 \(W/W_I\) 里的代表元作用在上面,然后去 \(L\) 里面查找对应的下标。
最终得到的图像如下图,计算了 30517 个顶点,42057 条边,11541 个多边形:

在上面的过程中,我们其实还用到了一个重要的计算:
问题 3.2: 给定任一单词 \(w\),怎样计算 \(w\) 的规范表示?怎样计算 \(w\) 关于某个标准椭圆子群 \(W_I\) 的陪集代表元?
同样我把解释放在附录里面。
关于代码
整个代码主要包含如下的功能:
Coxeter 群的计算。这部分由
coxeter模块中的CoxeterGroup类实现。Coxeter 群的计算又包含如下几个部分:- 计算 Coxeter 群的极小根反射表。
- 计算 Coxeter 中群元素的乘法,并返回结果的规范表示。
- 计算群元素关于给定标准椭圆子群的陪集代表元,并返回结果的规范表示。
- 计算识别 \(\mathcal{SL}(W)\) 的有限状态机,将其最小化,并绘制状态机。
密铺的绘制。主要是在
tiling.py文件中实现。它包含如下步骤:- 对给定的 Coxeter 群和指定的初始顶点位置,计算反射镜面和基本区域。
- 计算所有顶点的规范表示,以及边和面的连接关系。
- 将规范表示作用在初始顶点上得到所有顶点的浮点坐标。这些计算都是在高一维的射影模型中进行,因为这时反射都是线性变换,可以避免使用仿射变换和反演。然后投影到二维。
- 调用绘图库绘制密铺。
其中绘制 \(\mathcal{SL}(W)\)
的有限状态机需要使用 pygraphviz 模块,这个模块依赖于
graphviz 软件和
libgraphviz-dev。
将有限状态机最小化我参考的是 Gries 的文章。Gries 的文章写的很棒,但是我认为他并没有把存储 \((B,a)\) 对的列表性质讲清楚。
双曲情形的绘图我用的是一个叫 hyperbolic 的三方库。我对这个库其实不太满意,然而我一时也没有精力分出来再写一个,所以暂且先凑合着。这个库最大的好处是,它可以绘制具有常双曲宽度的边,即所谓的 hypercycle。
计算极小根的算法是这个代码中最大的性能陷阱。其中在判断一个极小根 \(\gamma\) 经过一个单反射 \(s_\alpha\) 以后是不是仍然是极小根时,采用的方法是判断 \(s_\gamma\) 和 \(s_\alpha\) 是不是生成一个有限群,即判断 \(s_\gamma s_\alpha\) 在单根 \(\Delta\) 下对应的矩阵是不是经过某次幂以后成为单位矩阵。这里面矩阵的元素都是分圆域里的代数整数,形如 \(p(\xi)\),其中 \(p(x)\) 是一个不可约整系数多项式,\(\xi\) 是本原 \(m\) 次单位根,其中 \(m\) 是 Coxeter 矩阵中所有元素的最大公倍数乘以 2。\(\xi\) 可以用分圆多项式 \(\Phi_m(x)\) 来描述。于是矩阵的计算被归结为 \(\mathbb{Z}[x]/(\Phi_m(x))\) 中的多项式运算。这个计算量非常依赖于 \(m\) 的值:例如对 (19, 20, 21) 这样的三角群,\(\Phi_m(x)\) 的表达式非常复杂,计算速度就很慢了。这一点与逆像素反射方法是不同的,逆像素反射法的计算量几乎不随群的变化而变化。
一种更合理的实现方法见 这里。
附录:对若干关键点的解释
在这里我简单回答前面正文中埋下的 问题 3.1 和 问题 3.2。这部分内容需要你了解 Coxeter 群的几何实现、Tits 锥、根系等预备知识,这部分内容可以参考 Humphreys 的教材。
仍然以 (7, 2, 3) 这个群为例子,先看下图:
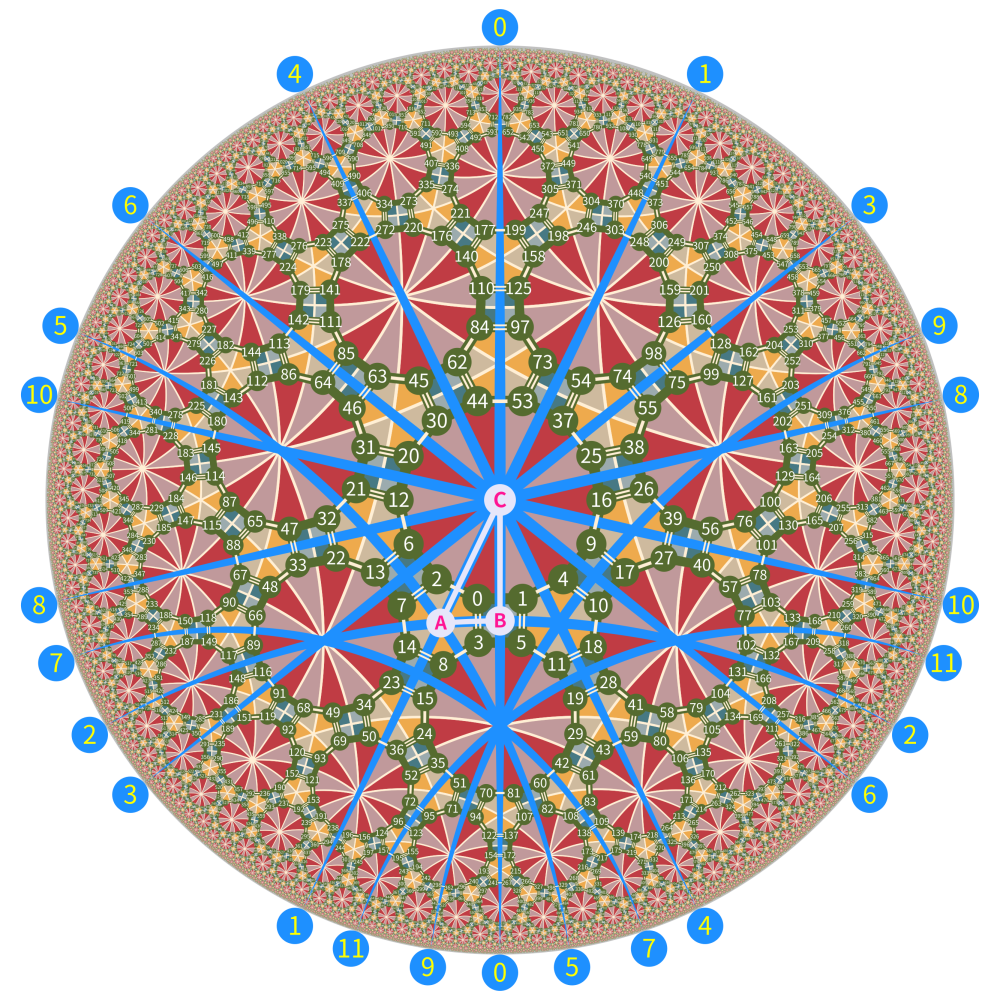
这个图和上图一样,只不过多了 12 个标记出的镜面,这 12 个镜面有特殊的含义:它们是群 \(W\) 的根系中的 12 个极小根。
你可以把 \(W\) 的根系理解为图中所有的圆弧,每个圆弧都是一个反射镜面,这些镜面都是 \(\Delta ABC\) 三条边所在的初始镜面 \(AB,AC,BC\) 在群 \(W\) 作用下的结果。每个镜面有正反两面,其中基本区域 \(\Delta ABC\) 所在的那一面是镜子的正面,另一面是背面。镜子正面的法向量给出一个正根,背面对应的法向量是将该正根取负(负根)。
我们总是用一个镜子的正法向量(正根)来指代这面镜子。
从直观上说,极小根 \(\gamma\) 是那些满足如下条件的镜面:假设一个人站在 \(\Delta ABC\) 的内部往外看,则不存在任何镜面 \(\beta\ne\gamma\) 完全挡在 \(\gamma\) 前面,使得这个人看不到 \(\gamma\) 的任何一点。这个话反过来说就是,如果这个人要从 \(\Delta ABC\) 的内部出发,走到 \(\gamma\) 的背面去,无论他怎么走都必须先跨过另一个镜子 \(\beta\ne \gamma\),那么 \(\gamma\) 就不是极小根。
单根必然都是极小根,因为它们是基本区域的边界,不可能还有镜子挡在它们和基本区域之间。
关于极小根的一个重要事实是,任何有限生成 Coxeter 群的极小根的个数都是有限的。这个结论在 Brink 和 Howlett 的证明中起到最关键的作用。
极小根的反射表 reftable 定义如下:它是一个二维数组,其第
\(i\) 行对应第 \(i\) 个极小根 \(\alpha_i\),其第 \(j\) 列对应第 \(j\) 个生成元 \(s_j\),其 \((i,
j)\) 位置填入的是 \(\beta=s_j(\alpha_i)\) 的结果:
- 如果 \(\beta=\alpha_k\) 是第 \(k\) 个极小根,则填入 \(k\)。
- 如果 \(\beta\) 是一个负根
(此情形发生当且仅当 \(\alpha_i\) 是第
\(j\) 个单根),则填入
-1。 - 如果 \(\beta\)
是一个正根,但不是极小根,则填入
None。
(7, 2, 3) 群的极小根反射表如下:
| root | \(s_0\) | \(s_1\) | \(s_2\) |
|---|---|---|---|
| 0 | -1 | 3 | 0 |
| 1 | 4 | -1 | 5 |
| 2 | 2 | 5 | -1 |
| 3 | 6 | 0 | 7 |
| 4 | 1 | 8 | 9 |
| 5 | 9 | 2 | 1 |
| 6 | 3 | 10 | 11 |
| 7 | 11 | 7 | 3 |
| 8 | 10 | 4 | None |
| 9 | 5 | None | 4 |
| 10 | 8 | 6 | None |
| 11 | 7 | None | 6 |
设 \(W\) 的所有极小根之集为 \(\Sigma\),\(\mathcal{SL}(W)\) 的有限状态机 \(\mathcal{A}\) 由如下规则给出:
\(\mathcal{A}\) 的状态是 \(\Sigma\) 的子集,其中初始状态为空集 \(\emptyset\)。
从一个状态 \(S\) 转移到另一个状态 \(S'\) 的规则为:
\[S\xrightarrow{\ s_i\ } \{s_i\} \cup (s_i(S)\cup\{ s_i(\alpha_j),j<i\})\cap\Sigma.\]
我们可以用宽度优先搜索找到所有的状态以及它们之间的转移关系,然后用 Hopcroft 算法 将得到的有限状态机最小化。
下图显示的是 (7, 2, 3) 这个群的状态机 \(\mathcal{A}\),每个状态的标号反映了它是
\(\Sigma\) 的哪个子集,例如
9 : {1, 2, 3, 5} 表示这个状态的编号是 9,它是由第 1, 2, 3,
5 个极小根构成的集合。

计算两个群元素乘法的规范表示的算法来自
Casselman。这个讲解起来可就太费功夫了,我可能未来需要专门再开一篇文章介绍。其代码如下,其中
s 是一个生成元,word
是一个逆最短字典序下的单词
(逆最短字典序就是把最短字典序中的单词反过来),函数返回的也是对应结果在逆最短字典序下的规范形式:
1 | |
由此函数不难计算任何两个单词相乘的逆最短字典序下的规范形式,倒过来自然也就解决了最短字典序下的乘法问题。
这里先在逆字典序下计算然后再倒过来获得字典序是为了和 Casselman 的文章中的论述保持一致。
计算一个规范表示的单词 word
关于某个标准椭圆子群的陪集是最简单的:设 \(W_T\) 是一个标准椭圆子群,其生成元是 \(W\) 的生成元 \(S\) 的一个子集 \(T\),则计算 word 关于 \(W_T\) 的左陪集代表元的伪代码如下:
1 | |
其中 \(l(\cdot)\) 是 Coxeter
群上的长度函数。这个算法会把 word 分解为形如 \(x^T\cdot w_T\) 的形式,其中 \(w_T\in W_T\),且对任何 \(t\in T\) 有 \(l(x^Tt)>l(x^T)\)。最终得到的陪集代表元
\(x^T\) 是规范表示。
对有限 Coxeter 群,其所有正根都是极小根;对仿射 Coxeter 群,其根系由一些平行的镜面族构成,每族镜面中的反射镜面互相平行。每个族中存在一对极小根,它们把基本区域 \(\Delta ABC\) 夹在中间并完全挡住本族中外面的镜面,所以只有它俩才是极小根。下图显示的是 (6, 2, 3) 密铺 (对称群为仿射 \(\widetilde{G}_2\)) 的 12 个极小根:

参考文献
关于 Coxeter 群中的计算,我主要参考的是 Casselman 的三篇文章:
Automata to perform basic calculations in Coxeter groups, by Bill Casselman.
Computation in Coxeter groups I. Multiplication, by Bill Casselman.
Computation in Coxeter groups II. Constructing minimal roots, by Bill Casselman.
关于 Coxeter 群的自动性质,可以参考 Brink & Howlett 的论文:
关于 Coxeter 群的基础知识,毫无疑问应该参考 Humphreys 的经典教材


