Coxeter 群笔记(一):抽象 Coxeter 群与几何实现
抽象 Coxeter 群
设 \(S\) 是一个集合,一个基于 \(S\) 的 Coxeter 矩阵 \(M=(m_{s,t})_{s,t\in S}\) 是一个对称矩阵,其对角线上都是 1,非对角线元素取值于 \(\{2,3,\ldots,\infty\}\)。\(|S|\) 叫做 \(M\) 的秩 (rank)。在这个系列中我们只考虑 \(|S|<\infty\) 的情形。
矩阵 \(M\) 确定了一个有限表现群 \(W\),其生成元为集合 \(S\),群表现如下: \[W = \langle s\in S\ |\ (st)^{m_{s,t}}=1\ {\rm if}\ m_{s,t}<\infty\rangle.\]
也就是说,\(S\) 满足以下的生成关系:
- 对任何 \(s\in S\) 有 \(s^2=1\)。
- 对任何 \(s\ne t\) 且 \(m_{s,t}<\infty\) 有辫关系 (braid relation) \[\overbrace{sts\cdots}^{m_{s,t}}=\overbrace{tst\cdots}^{m_{s,t}}\] 成立。(当 \(m_{s,t}=\infty\) 时不引入任何关系)
我们称 \((W, S)\) 是一个 Coxeter 系,\(W\) 是一个有限生成 Coxeter 群。
注: 我们总是用 \((W,S)\) 来表示一个 Coxeter 群。即在提到一个 Coxeter 群 \(W\) 时,需要同时指明其生成元集合 \(S\)。这是因为,可能存在不同的集合 \(S\),它们给出同一个 \(W\)。但是像长度函数 \(l(w)\)、根系、Bruhat 序这些重要的概念,只有在指定生成元集 \(S\) 的前提下才有意义。
用 Coxeter 矩阵或者群表现来描述 Coxeter 群还是太不方便了。我们可以用一个有限图 \(\Gamma\) 更直观地表示 \((W,S)\),\(\Gamma\) 叫做 \((W,S)\) 的 Coxeter 图:
- \(\Gamma\) 的顶点集是 \(S\)。
- 如果 \(m_{s,t}\ne 2\),就在顶点 \(s\) 和 \(t\) 之间连一条边,并且给这条边标上记号 \(m_{s,t}\)。
- 但是如果 \(m_{s,t}=3\) 的话,就省略这个记号不写。
此外如果 \(\Gamma\) 是连通的,就称 \((W,S)\) 是不可约的。
例: Coxeter 矩阵 \[\begin{pmatrix}1 & 4 & 2\\4&1&3\\2&3&1\end{pmatrix}\] 对应的 Coxeter 图 \(\Gamma\) 是

\(\Gamma\) 是连通的,所以 \(W\) 是不可约的。这个群是三维正方体的对称群:
去掉最后一个顶点,前两个顶点构成二面体群 \(D_4\),\(D_4\) 是正四边形的对称群,对应正方体的每个面是正四边形;去掉第一个顶点,后两个顶点构成二面体群 \(D_3\),\(D_3\) 是正三角形的对称群,对应每个顶点处有 3 个面相遇。
例: 设 \(m\geq4\) 是正整数,Coxeter 矩阵 \[\begin{pmatrix}1 & m & 2\\m&1&2\\2&2&1\end{pmatrix}\] 对应的 Coxeter 图 \(\Gamma\) 是
\(\Gamma\) 有两个连通分支,所以 \(W\) 是可约的。这个群是三维空间中棱柱的对称群,前两个相邻的顶点给出二面体群 \(D_m\),它负责在 \(xy\) 平面内生成正 \(m\) 边形;最后的孤立顶点在 \(z\) 轴方向上将多边形作反射形成棱柱结构:
例: Coxeter 矩阵 \[\begin{pmatrix}1 & 3 & 4\\3&1&\infty\\4&\infty&1\end{pmatrix}\] 对应的 Coxeter 图 \(\Gamma\) 是

\(\Gamma\) 是连通的,所以 \(W\) 是不可约的。这个群给出的是双曲空间中的密铺:

例: Coxeter 矩阵 \[\begin{pmatrix}1 & 5 & 2 & 2\\5&1&3&2\\2&3&1&4\\2&2&4&1\end{pmatrix}\] 对应的 Coxeter 图 \(\Gamma\) 是
\(W\) 是不可约的。这个群给出的是三维双曲空间中的密铺:
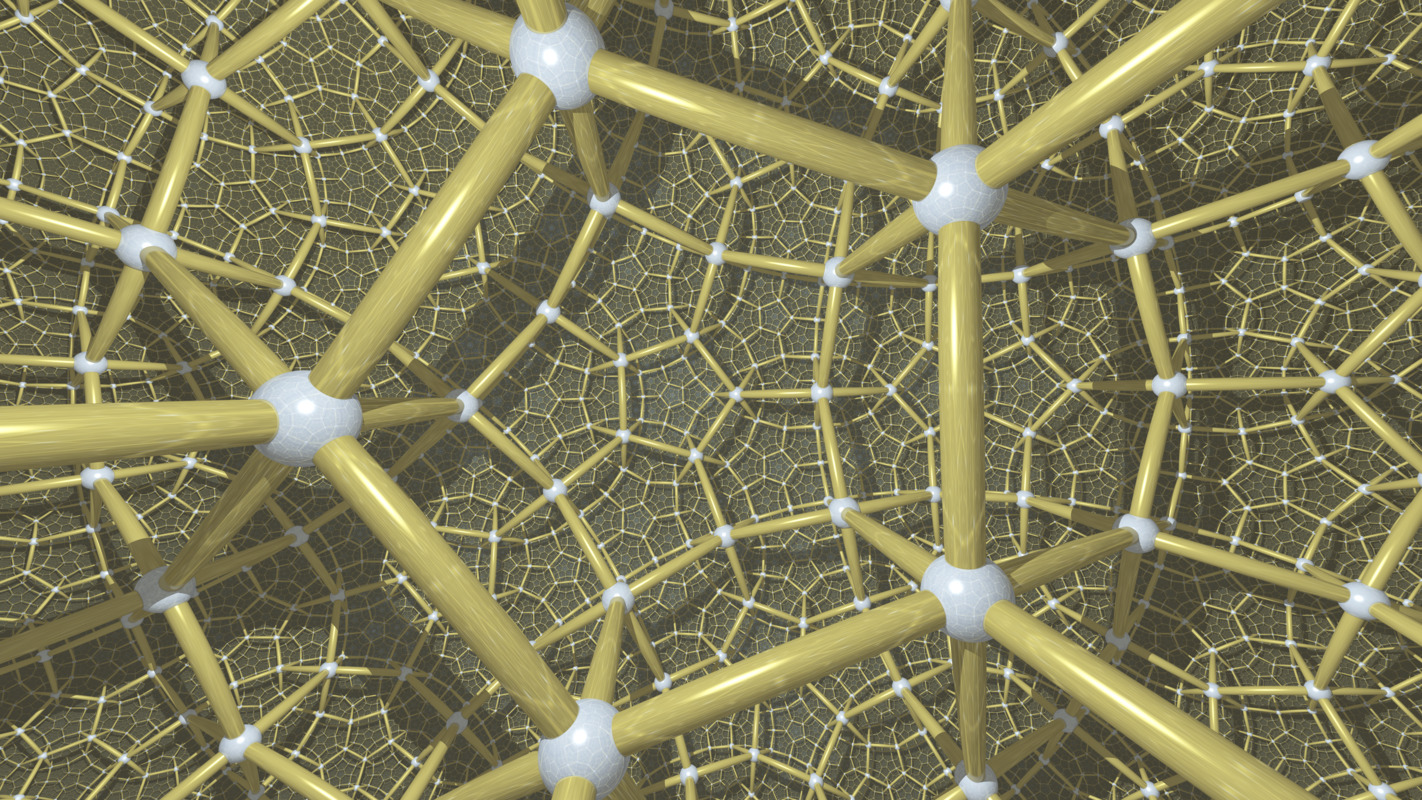
去掉最后一个顶点,前三个顶点给出正十二面体的对称群 \((5,3)\),说明这个密铺由正十二面体组成;去掉第一个顶点,剩下三个顶点给出正方体的对称群 \((3,4)\cong(4,3)\),说明每个顶点处有 8 个正十二面体相遇。
我们主要关心 \(\Gamma\) 不可约的情形。因为如果 \(\Gamma=\Gamma_1\cup\cdots\cup\Gamma_k\,(k>1)\) 包含多个连通分支的话,那么对任何 \(s\in\Gamma_i\) 和 \(t\in\Gamma_j\) 有 \(m_{s,t}=2\),即 \(st=ts\),于是 \(\Gamma_i\) 中的生成元与 \(\Gamma_j\) 中的生成元两两交换,这时 \(W\) 有直积分解 \[W=W_1\times\cdots\times W_k.\] 其中 \(W_1,\ldots,W_k\) 分别是子图 \(\Gamma_1,\ldots,\Gamma_k\) 对应的 Coxeter 群。所以我们只要研究 \(\Gamma\) 不可约的情形即可。
还有一种给 \(\Gamma\) 的边标号的方式,叫做 Vinberg 记号,它允许给 \(m_{s,t}=\infty\) 的边用 \(\leq-1\) 的实数作为标号。比如像下面这样:
该图表示的抽象 Coxeter 群和前面的 \(\Delta(3,4,\infty)\) 相同,但其中 \(\infty\) 边的标号变成了 \(-1.1\)。我后面会解释,这种标号方式其实是指定了几何实现中两个镜面的「双曲距离」。我们在后文介绍 Boyd-Maxwell 球堆时也会采用这种记号。
Coxeter 图除了直观上的好处外,还能传达更多信息。比如,当 \(\Gamma\) 包含回路,或者包含某个度数 \(\geq4\) 的顶点时,我们可以立刻知道 \((W,S)\) 一定是无限群 (Humphreys 1990, sec. 2.7)。更进一步,一个 Coxeter 群是否能够产生 Boyd-Maxwell 球堆,也完全可以从其 Coxeter 图中读出来。
长度函数
对 \(W\) 中的任一元素 \(w\),存在许多种不同的方式将 \(w\) 表示为 \(S\) 中生成元的乘积。在所有这些表示中,长度最短者叫做 \(w\) 的既约表示:即,如果 \(w=s_1s_2\cdots s_k\) 是一个长度为 \(k\) 的表示,且 \(w\) 不存在任何长度小于 \(k\) 的表示,就称该表示是 \(w\) 的既约表示。既约表示未必唯一,但它们都具有相同的长度。定义 \(l(w)\) 为 \(w\) 的任意一个既约表示的长度。
\(l(w)\) 具有如下的性质:
- \(l(xy)\leq l(x) + l(y)\)。
- \(l(w) = l(w^{-1})\)。
- \(l(w)=0\) 当且仅当 \(w=1\)。
- \(l(ws)=l(w)\pm 1\),其中 \(w\in W, s\in S\)。
前三点都是显然的,只有 4 需要证明。显然 \(|l(ws)-l(w)|\leq 1\),所以只要说明 \(l(ws)\) 和 \(l(s)\) 不相等即可。这一步需要用到自由群的泛性质:
设 \(F\) 是由集合 \(S\) 生成的 自由群,定义群同态 \({\rm sgn}: F\to{\pm1}\) 如下:对 \(F\) 的每个生成元 \(s\in S\) 规定 \({\rm sgn}(s)=-1\),然后将此映射扩充为 \(F\) 到 \({\pm1}\) 的群同态。容易验证 \((W,S)\) 的所有生成关系都属于这个同态的核,因此根据 自由群的泛性质,\({\rm sgn}\) 诱导了一个从 \((W,S)\) 到 \({\pm1}\) 的群同态。若 \(w=s_1s_2\cdots s_k\) 是 \(w\) 的任一既约表示,则 \[{\rm sgn}(w)={\rm sgn}(s_1){\rm sgn}(s_2)\cdots{\rm sgn}(s_k)=(-1)^k=(-1)^{l(w)}.\] 从而 \({\rm sgn}(ws)={\rm sgn}(w){\rm sgn}(s)=-{\rm sgn}(w)\),这说明 \(l(ws)\ne l(w)\),从而第 4 条成立。
几何实现
抽象 Coxeter 群是通过生成元和生成关系定义的,直接从这种定义出发研究群结构是非常困难的。本节将介绍如何将一个抽象的 Coxeter 群实现为内积空间中的正交反射群,从而可以使用几何、线性代数等多种工具来研究它。
设 \((W,S)\) 是一个 Coxeter 系,\(M=(m_{s,t})_{s,t\in S}\) 是 Coxeter 矩阵。令 \(V\) 是一个维数为 \(n=|S|\) 的实向量空间,其一组基为 \(\{\alpha_s \mid s\in S\}\)。我们规定 \(V\) 上的内积 \((\cdot,\cdot)\) 如下:
\[(\alpha_s,\alpha_t)=\begin{cases} 1 & s=t,\\ -\cos(\pi/m_{s,t}) & m_{s,t}<\infty,\\ -a_{s,t} & m_{s,t}=\infty.\end{cases}\] 这里 \(a_{s,t}=a_{t,s}\geq1\) 是实数,它对应的是 \(\infty\) 边的 Vinberg 记号。不同的 \(s,t\) 对可以使用不同的 \(a_{s,t}\)。
根据定义 \((\alpha_s,\alpha_s)=1\),即每个 \(\alpha_s\) 都是单位向量。
注: \(a_{s,t}=1\) 表示 Euclidean 空间中两个平行的镜面(或者双曲空间中两个平行的镜面);\(a_{s,t}>1\) 表示双曲空间中两个超平行的镜面;\(2\leq m_{s,t}<\infty\) 表示两个相交的镜面。
下图显示了对前面的 \(\Delta(3,4,\infty)\) 群,对标号为 \(\infty\) 的边取 \(a_{s,t}=1.15\) 时给出的效果:

你可以看到每个三角形都不再是封闭的,它们的墙壁中有两条「超平行」的测地线,这两条测地线交点落在双曲空间的外面。
内积 \((\cdot,\cdot)\) 未必是通常的 Euclidean 内积,即它未必是正定的。但我们最关心的情形有三种:
- 如果 \((\cdot,\cdot)\) 是正定的,就称 \((\cdot,\cdot)\) 是有限型的;
- 如果 \((\cdot,\cdot)\) 是半正定的,但不是正定的,就称 \((\cdot,\cdot)\) 是仿射型的;
- 如果 \((\cdot,\cdot)\) 的符号是 \((n-1, 1)\),就称 \((\cdot,\cdot)\) 是双曲型的。
除此之外的情况,统称为不定型。
给定 \(s\in S\),定义 \(V\) 上的反射 \(\rho_s\) 为 \[\rho_s(v) = v -2(v,\alpha_s)\alpha_s ,\quad v\in V.\] 容易验证,\(\rho_s\) 满足以下性质:
- \(\rho_s(\alpha_s)=-\alpha_s\);
- \(\rho_s\) 保持超平面 \(\{v\in V\mid (v,\alpha_s)=0\}\) 上的点不动;
- \(\rho_s\) 保持 \((\cdot,\cdot)\) 不变:\((\rho_s(u),\rho_s(v)) = (u,v),\,\forall u,v\in V\)。
因此 \(\rho_s\in \mathrm{O}(V)\) 是以 \(\alpha\) 为法向量的镜面反射。
我们来证明 \(s\to\rho_s\) 实际上给出了 \((W,S)\) 到 \(\mathrm{O}(V)\) 的群同态,从而得到了一个线性表示 \[\rho: W\to\rho(W)\leqslant\mathrm{O}(V)\] 为此,只需验证 \(\{\rho_s\mid s\in S\}\) 满足与 \((W,S)\) 相同的生成关系即可,这样根据商群的泛性质,即得存在群同态 \(W\to\mathrm{O}(V)\) 将每个 \(s\) 映射到 \(\rho_s\)。即我们只要证明:
命题 3.1. \((\rho_s\rho_t)^{m_{s,t}}=1\) 对任何 \(s,t\in S\) 成立。
这个结论的证明在 (Humphreys 1990, sec. 5.3) 和 (Howlett 1996) 中都可以找到,但我更喜欢 Howlett 的做法,把 rank 2 情形的根系具体的算出来。这是最简单,但又非平凡的根系的例子,熟悉它的重要性怎么强调也不为过。
证明:当 \(s=t\) 时所证即为 \(\rho_s^2=1\),由于 \(\rho_s\) 是反射这当然是成立的。
下设 \(s\ne t\),记 \(V_{s,t}={\rm span}\{\alpha_s,\alpha_t\}\),并记 \(V_{s,t}^\perp\) 是 \(V_{s,t}\) 在 \((\cdot,\cdot)\) 下的正交补。不难验证 \(\rho_s\) 和 \(\rho_t\) 限制在 \(V_{s,t}^\perp\) 上都是恒等变换。
注意,未必有 \(V=V_{s,t}\oplus V_{s,t}^\perp\) 成立,因为 \((\cdot,\cdot)\) 可能是退化的。但是如果 \((\cdot,\cdot)\) 限制在 \(\mid_{V_{s,t}}\) 是非退化的,那么就有 \(V=V_{s,t}\oplus V_{s,t}^\perp\) 就成立。这是双线性型的基本结论。
我们来计算 \(\sigma=\rho_s\rho_t\) 的阶。记 \(m=m_{s,t}\),分情况讨论:
1. \(m<\infty\)
这时 \((\cdot,\cdot)\) 限制在 \(V_{s,t}\) 上的 Gram 矩阵是 \[\begin{pmatrix}1&-\cos\theta\\-\cos\theta&1\end{pmatrix},\quad \theta=\frac{\pi}{m}.\] 这个矩阵是正定的,从而 \((\cdot,\cdot)\mid_{V_{s,t}}\) 非退化,从而 \(V=V_{s,t}\oplus V_{s,t}^\perp\) 成立,而 \(\sigma\) 限制在正交补 \(V_{s,t}^\perp\) 上是恒等变换,因此 \(\sigma\) 在 \(V\) 上的阶就等于它在 \(V_{s,t}\) 上的阶。
为了简化记号,令 \(a_k=\sin (k\theta)/\sin\theta\),直接计算如下: \[\begin{aligned} &\alpha_s\xrightarrow{\ \rho_t\ }a_1\alpha_s+a_2\alpha_t\xrightarrow{\ \rho_s\ }a_3\alpha_s+a_2\alpha_t\xrightarrow{\ \rho_t\ }a_3\alpha_s+a_4\alpha_t\xrightarrow{\ \rho_s\ }\cdots\\ &\alpha_t\xrightarrow{\ \rho_s\ }a_2\alpha_s+a_1\alpha_t\xrightarrow{\ \rho_t\ }a_2\alpha_s+a_3\alpha_t\xrightarrow{\ \rho_s\ }a_4\alpha_s+a_3\alpha_t\xrightarrow{\ \rho_t\ }\cdots \end{aligned} \] 这两个链的周期都是 \(2m\),因为它们的第 \(2m+1\) 项各自回到了初始状态: \[\begin{aligned} a_{2m+1}\alpha_s+a_{2m}\alpha_t&=\dfrac{\sin (2m+1)\theta}{\sin\theta}\alpha_s+\dfrac{\sin (2m)\theta}{\sin\theta}\alpha_t=\alpha_s,\\ a_{2m}\alpha_s+a_{2m+1}\alpha_t&=\dfrac{\sin (2m)\theta}{\sin\theta}\alpha_s+\dfrac{\sin (2m+1)\theta}{\sin\theta}\alpha_t=\alpha_t. \end{aligned}\] 因此 \(\sigma\) 的阶等于 \(m\)。
2. \(m=\infty\)
这时未必有 \(V=V_{s,t}\oplus V_{s,t}^\perp\)。但我们可以证明 \(\sigma\) 在 \(V_{s,t}\) 上的阶是无穷,那么自然它在 \(V\) 上的阶也是无穷。
设 \(\theta\geq0\) 使得 \(a_{s,t}=\cosh\theta\)。记 \(b_k=\sinh(k\theta)/\sinh\theta\),直接计算: \[\begin{aligned} &\alpha_s\xrightarrow{\ \rho_t\ }b_1\alpha_s+b_2\alpha_t\xrightarrow{\ \rho_s\ }b_3\alpha_s+b_2\alpha_t\xrightarrow{\ \rho_t\ }b_3\alpha_s+b_4\alpha_t\xrightarrow{\ \rho_s\ }\cdots\\ &\alpha_t\xrightarrow{\ \rho_s\ }b_2\alpha_s+b_1\alpha_t\xrightarrow{\ \rho_t\ }b_2\alpha_s+b_3\alpha_t\xrightarrow{\ \rho_s\ }b_4\alpha_s+b_3\alpha_t\xrightarrow{\ \rho_t\ }\cdots\end{aligned} \] 当 \(a_{s,t}=1\) 时 \(\theta=0\),\(b_k\) 应当理解为 \(\lim_{\theta\to0}\sinh(k\theta)/\sinh(\theta)=k\)。
这两个链条永不重复,所以 \(\sigma\) 的阶是无穷。
至此命题得证。\(\blacksquare\)
后面我们会看到,\(W\xrightarrow{\rho}\rho(W)\) 实际上是群同构,这样就把抽象的 Coxeter 群 \(W\) 实现为具体的反射群 \(\rho(W)\)。研究 \(\rho(W)\) 并不会丢失 \(W\) 的信息。
最后是一个记号的简化:把 \(w\in W\) 在 \(V\) 上的作用记为 \(wv\,\colon=\rho(w)(v)\)。


