春节的晚上，外面鞭炮喧天，家人在看电视，我躲在屋里看数学，还是挺惬意的。

我正在看的是 John Baez 和 Greg Egan 的博客。John Baez 是一位在科普方面非常高产的数学家，写过不计其数的科普文章。读他的文章非常让人享受：他很喜欢从直观的例子入手，一步步启发读者，展开到更高级的数学。尤其是他行文的风格，字里行间都洋溢着他对所讨论的数学对象的喜爱。Greg Egan 是澳大利亚的一位非常高产的科幻小说作家，有不少作品已经被国内引入。他的小说属于硬科幻风格，而且是非常硬的那种。他的 博客文章 同样精彩！不过与 John Baez 不同的是，Greg Egan 的文章不太会去兼顾不同水平的读者，对我来说，要看懂他在说什么经常不是一件容易的事情。

John Baez 博客上有一个系列 Rolling circles and balls 讨论了圆的外摆线和焦散，Greg Egan 也有一篇 文章 更深入的讨论了曲线的焦散。这个话题非常有意思，我也一时手痒写了代码实验了一番并记录在此。

POV-Ray 光学实验

有个有趣的物理现象，当光线照在咖啡杯的内壁上时，光线反射以后会形成一个亮斑，术语叫做焦散 (caustic)。

形成焦散的原因是，光线在杯子内壁反射以后，光子的分布是不均匀的，某些区域经过的光子特别密集，所以亮度就更高。

焦散是一条曲线，它和所有的反射光线相切，即它是所有反射光线的包络 (envelope)。焦散的具体形状和杯子的形状、光源的位置都有关。假设杯子是圆形的，则当光源是一个点光源且恰好位于杯子边缘上某一点时，得到的焦散叫做 心脏线 (cardioid)。当光源位于无穷远时（可以视作平行光源），得到的焦散是 肾形线 (nephroid)。一般情况下焦散的形状介于心脏线和肾形线之间。

更有意思的是，如果杯子的外形是心脏线，而且光源正好位于心脏线的尖点时，得到的焦散正好是肾形线。我写了一个 POV-Ray 脚本，模拟了这一现象：

圆形杯子给出心脏线	心脏线杯子给出肾形线

值得注意的是，心脏线和肾形线都是所谓的 外摆线，只是两圆的半径之比不同：

所以我们很容易作出如下的猜想：如果在肾形线的内部或者尖点放一个光源，是不是又会得到下一个外摆线？然而根据 Greg Egan 在他博客中的实验，这个应该是不成立的。

理论上这个 POV-Ray 脚本可以渲染任意的参数曲线反射的效果，但是 POV-Ray 渲染 parametric surface + radiosity 非常慢，所以如果你想试一试的话，最好还是用 POV-Ray 原生的 CSG 来构造镜面曲线。

求解参数曲线的焦散

这一节我们来介绍怎样计算一般的参数曲线 \(\mathbf{c}(t)=(x(t),y(t))\) 的焦散曲线。

设点光源的位置是 \((a,b)\)，则在曲线上的一点 \((x,y)\) 处，入射光线的方向是 \[\mathbf{l}=(x-a,y-b).\] 不需要把 \(\mathbf{l}\) 单位化，因为我们列方程的时候只需要光线的方向，并不在乎长度。

同样是在 \((x,y)\) 处，曲线的法向量是 \[\mathbf{n}=\frac{(-y', x')}{\sqrt{(x')^2+(y')^2}}=\frac{(-y', x')}{|\mathbf{c}'|}.\] 这里我们用 \(x',y'\) 表示 \(x,y\) 关于 \(t\) 的导数。

于是 \((x,y)\) 处的反射光线的方向 \(\mathbf{r}\) 由如下反射公式给出： \[\mathbf{r}= \mathbf{l}- 2(\mathbf{l}\cdot \mathbf{n})\mathbf{n}.\] 设 \((X,Y)\) 是反射光线上的任一点，由于 \((x,y)\) 是反射光线的起点，所以 \((X-x,Y-y)\) 与 \(\mathbf{r}\) 平行。记 \(\mathbf{r}=(r_x,r_y)\)，则 \((X-x,Y-y)\) 与 \((-r_y, r_x)\) 垂直，即 \[(X-x, Y-y)\cdot(-r_y, r_x)=0.\] 记 \[F(X,Y,t)=(X-x, Y-y)\cdot(-r_y, r_x),\] 则我们得到了反射光线 \((X(t), Y(t))\) 满足的曲线族方程 \(F(X,Y,t)=0\)。于是焦散曲线可以通过联立方程组 \[\begin{align*}F(X,Y,t)=0,\\\frac{\partial F}{\partial t}F(X,Y,t)=0.\end{align*}\] 也就是 \[\begin{align*}(X-x, Y-y)\cdot(-r_y, r_x)&=0,\\-(x',y')\cdot(-r_y, r_x) + (X-x,Y-y)\cdot(-r_y', r_x') &=0.\end{align*}\] 然后解出 \(X,Y\) 得到。

如果你还记得 2x2 矩阵的逆公式的话，这个方程组其实可以目视写出解来。我们把它写成

\[\begin{pmatrix}-r_y & r_x\\ -r_y'&r_x'\end{pmatrix}\cdot\begin{pmatrix}X-x\\Y-y\end{pmatrix}=\begin{pmatrix}0\\ r_xy'-r_yx'\end{pmatrix}.\] 于是 \[\begin{align*}\begin{pmatrix}X-x\\Y-y\end{pmatrix}&=\begin{pmatrix}-r_y & r_x\\ -r_y'&r_x'\end{pmatrix}^{-1}\begin{pmatrix}0\\ r_xy'- r_yx'\end{pmatrix}\\ &=\frac{1}{r_xr_y'-r_yr_x'}\begin{pmatrix}r_x' & -r_x\\ r_y'&-r_y\end{pmatrix}\begin{pmatrix}0\\ r_xy'-r_yx'\end{pmatrix}\\ &=\frac{r_xy'-r_yx'}{r_yr_x'-r_xr_y'}\begin{pmatrix}r_x\\ r_y\end{pmatrix}.\end{align*}\] 即 \[\begin{pmatrix}X\\ Y\end{pmatrix}=\begin{pmatrix}x\\y\end{pmatrix} + \frac{r_xy'-r_yx'}{r_yr_x'-r_xr_y'}\begin{pmatrix}r_x\\ r_y\end{pmatrix}.\]

按照上面的理论，我写了一个小脚本，用 sympy (version=1.12) 来计算圆的焦散线。其中圆的中心在原点，半径为 1，光源在 \((1,0)\) 处。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

from sympy import *

t, X, Y = symbols("t X Y")
C = Matrix([cos(t), sin(t)]) # curve
light = Matrix([1, 0]) # light source
l = C - light # incident ray
dx, dy = diff(C, t)
n = Matrix([dy, -dx]) # normal vector
r = simplify(l - 2 * l.dot(n) * n / n.dot(n)) # reflected ray
F = (Y - y) * r[0] - (X - x) * r[1]
dF = diff(F, t)
result = solve((F, dF), X, Y) # solve the envelope
print(f"X(t)={trigsimp(result[X], method='groebner')}")
print(f"Y(t)={trigsimp(result[Y], method='groebner')}")

sympy 给出的结果是：

1
2

X(t)=2*cos(t)/3 + cos(2*t)/3
Y(t)=2*sin(t)/3 + sin(2*t)/3

这正是喜闻乐见的心脏线的参数表示： \[\left\{\begin{align*}x(t)&=\frac{\cos(2t) + 2\cos(t)}{3},\\ y(t)&=\frac{\sin(2t) + 2\sin(t)}{3}.\end{align*}\right.\]

使用这个参数表示，我们继续计算当光源放在心脏线的尖点，即 \(t=\pi\) 对应的点 \((-\frac{1}{3},0)\) 时得到的焦散：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

from sympy import *

t, X, Y = symbols("t X Y")
C = Matrix([(2*cos(t) + cos(2*t)) / 3, (2*sin(t) + sin(2*t)) / 3])
light = Matrix([S('-1/3', evaluate=False), 0])
l = C - light # incident ray
dx, dy = diff(C, t)
n = Matrix([dy, -dx]) # normal vector
r = simplify(l - 2 * l.dot(n) * n / n.dot(n)) # reflected ray
F = (Y - y) * r[0] - (X - x) * r[1]
dF = diff(F, t)
result = solve((F, dF), X, Y) # solve the envelope
print(f"X(t)={trigsimp(result[X], method='groebner')}")
print(f"Y(t)={trigsimp(result[Y], method='groebner')}")

sympy 很快算出了正确的结果：

1
2

X(t)=sin(t)*sin(2*t)/3 + cos(t)/3
Y(t)=-sin(t)*cos(2*t)/3 + sin(t)/3

不难验证

\[\begin{align*}\frac{\sin(t)\sin(2t) + \cos(t)}{3}&=\frac{3\cos(t) - \cos(3t)}{6},\\ \frac{-\sin(t)\cos(2t) + \sin(t)}{3}&=\frac{3\sin(t) - \sin(3t)}{6}.\end{align*}\]

这正是 维基百科 在肾形线的参数方程中取 \(a=1/6\) 的表示。

把上面的曲线画出来是这样的：

求解多项式曲线的焦散

很多时候曲线的方程是通过隐函数 \(P(x,y)=0\) 的形式给出的，其中 \(P(x,y)\) 是关于两个变元 \(x,y\) 的多项式。这样的曲线叫做平面代数曲线。这时求解焦散要用到 Gröbner 基的工具。

让我们回到参数方程的情形，我们已经看到，这时焦散 \((X,Y)\) 有显示解

\[\begin{pmatrix}X\\ Y\end{pmatrix}=\begin{pmatrix}x\\y\end{pmatrix} + \frac{r_xy'-r_yx'}{r_yr_x'-r_xr_y'}\begin{pmatrix}r_x\\ r_y\end{pmatrix}.\]

其中 \(x,y,r_x,r_y\) 都是关于 \(t\) 的函数，它们的导数也是可计算的，所以可以算出 \((X,Y)\) 来。

但是在隐函数的情形，我们没有 \(x,y\) 的某种关于 \(t\) 的表达式。不过没关系，我们先假设有这样的参数表达式，看看能得到什么结论。设 \(x=x(t),y=y(t)\) 是某个参变元 \(t\) 的函数，在 \(P(x,y)=0\) 两边对 \(t\) 求导可得 \[\frac{\partial P}{\partial t}=\frac{\partial P}{\partial x}x'(t) + \frac{\partial P}{\partial y}y'(t)=0.\] 记 \(k=-\frac{\partial P}{\partial x}/\frac{\partial P}{\partial y}\)，则 \(y'(t)=kx'(t)\)。

对反射光线 \(\mathbf{r}\) 的两个分量 \(r_x,r_y\) 也分别使用链式求导，我们有 \[\begin{align*}\frac{\partial r_x}{\partial t}&=\frac{\partial r_x}{\partial x}x'(t) + \frac{\partial r_x}{\partial y}y'(t),\\ \frac{\partial r_y}{\partial t}&=\frac{\partial r_y}{\partial x}x'(t) + \frac{\partial r_y}{\partial y}y'(t).\end{align*}\] 于是我们发现比值 \[\begin{align*} \frac{r_xy'-r_yx'}{r_yr_x'-r_xr_y'}&=\frac{r_xk-r_y}{r_y(\frac{\partial r_x}{\partial x}+\frac{\partial r_x}{\partial y}k)-r_x(\frac{\partial r_y}{\partial x} + \frac{\partial r_y}{\partial y}k)}\\ &=-\frac{r_x\frac{\partial P}{\partial x}+r_y\frac{\partial P}{\partial y}}{r_y(\frac{\partial r_x}{\partial x}\frac{\partial P}{\partial y}-\frac{\partial r_x}{\partial y}\frac{\partial P}{\partial x})-r_x(\frac{\partial r_y}{\partial x}\frac{\partial P}{\partial y} - \frac{\partial r_y}{\partial y}\frac{\partial P}{\partial x})}.\end{align*}\] 变成了一个不需要显式用到 \(t\) 的量，即变量 \(t\) “消掉” 了。代入上面焦散的表达式中，我们得到 \[\begin{pmatrix}X\\ Y\end{pmatrix}=\begin{pmatrix}x\\y\end{pmatrix}-\frac{r_x\frac{\partial P}{\partial x}+r_y\frac{\partial P}{\partial y}}{r_y(\frac{\partial r_x}{\partial x}\frac{\partial P}{\partial y}-\frac{\partial r_x}{\partial y}\frac{\partial P}{\partial x})-r_x(\frac{\partial r_y}{\partial x}\frac{\partial P}{\partial y} - \frac{\partial r_y}{\partial y}\frac{\partial P}{\partial x})}\begin{pmatrix}r_x\\ r_y\end{pmatrix}.\] 这个式子还可以再简化一点：注意到曲线在 \((x,y)\) 处的法向量由 \(\mathbf{n}=\frac{\nabla P}{|\nabla P|}\) 给出，其中 \(\nabla P=(\frac{\partial P}{\partial x},\frac{\partial P}{\partial y})\)。于是由 \[\mathbf{r}= \mathbf{l}- 2(\mathbf{l}\cdot \mathbf{n})\mathbf{n}\] 可得 \[\mathbf{r}\cdot \nabla P=-\mathbf{l}\cdot \nabla P.\] 从而 \[\begin{pmatrix}X\\ Y\end{pmatrix}=\begin{pmatrix}x\\y\end{pmatrix}+\frac{\mathbf{l}\cdot\nabla P}{r_y(\frac{\partial r_x}{\partial x}\frac{\partial P}{\partial y}-\frac{\partial r_x}{\partial y}\frac{\partial P}{\partial x})-r_x(\frac{\partial r_y}{\partial x}\frac{\partial P}{\partial y} - \frac{\partial r_y}{\partial y}\frac{\partial P}{\partial x})}\begin{pmatrix}r_x\\ r_y\end{pmatrix}.\]

这是四个变量 \(x,y,X,Y\) 满足的两个方程，形如 \(F(X,x,y)=0\) 和 \(G(Y,x,y)=0\)。记住我们还有已知的方程 \(P(x,y)=0\)。为了从这三个方程中消掉 \(x,y\)，得到一个仅包含 \((X,Y)\) 的表达式，我们可以尝试用 Gröbner basis 方法。Gröbner 基方法会把多项式方程组 \[F=G=P=0\] 转化为一组等价的新方程组 \[g_1=g_2=\cdots=g_m=0.\] 即它们有完全相同的解集。

\(\{g_1,\ldots,g_m\}\) 是 \(F,G,P\) 在 4 个变元的多项式环 \(\mathbb{R}[x,y,X,Y]\) 中生成的理想 \(I=\langle F,G,P\rangle\) 的一组生成元，\(\{g_1,\ldots,g_m\}\) 叫做 \(I\) 的约化的 Gröbner 基。在字典序 \(x\succ y\succ X\succ Y\) 下，约化的 Gröbner 基会有一个好的属性，即从 \(g_1\) 变化到 \(g_m\) 时，多项式中的变元会按照从 \(x\to y\to X\to Y\) 的先后顺序被消除掉。注意这是个不太严格的说法，我们并不是总能消掉顺序靠前的变元，但是如果消除发生的话，它就会按照这个顺序来。这样我们就可以执行类似高斯消元法中的“回代”操作。从而新的方程组求解会比原方程组更加简单。

我们来用 sympy 实验一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

from sympy import *

x, y, X, Y = symbols("x y X Y")
P = x**2 + y**2 - 1
dx = diff(P, x)  # gradient of P
dy = diff(P, y)
curve = Matrix([x, y])
light_source = Matrix([1, 0])
l = curve - light_source  # the incident ray
n = Matrix([dx, dy])  # the normal vector
r = simplify(l - 2 * l.dot(n) * n / n.dot(n))  # the reflected ray
rx, ry = r
dxrx = diff(rx, x)
dyrx = diff(rx, y)
dxry = diff(ry, x)
dyry = diff(ry, y)
denominator = ry * (dxrx * dy - dyrx * dx) - rx * (dxry * dy - dyry * dx)
nominator = dx * l[0] + dy * l[1]
F = (X - x) * denominator - nominator * rx
G = (Y - y) * denominator - nominator * ry
eqs = [eq.as_numer_denom()[0] for eq in [F, G, P]]
gb = groebner(eqs, [x, y, X, Y])
print(gb)

sympy 给出的结果的最后一项是

\[27 X^{4} y^{2} + 54 X^{2} Y^{2} y^{2} - 18 X^{2} y^{2} - 8 X y^{2} + 27 Y^{4} y^{2} - 18 Y^{2} y^{2} - y^{2}.\]

\(x\) 被消掉了！原方程组 \(F=G=P\) 的解必然是上面这个方程的解的子集。观察它的每一项都带有一个 \(y^2\)，这显然不是我们要的解。把 \(y^2\) 去掉，剩下的因子

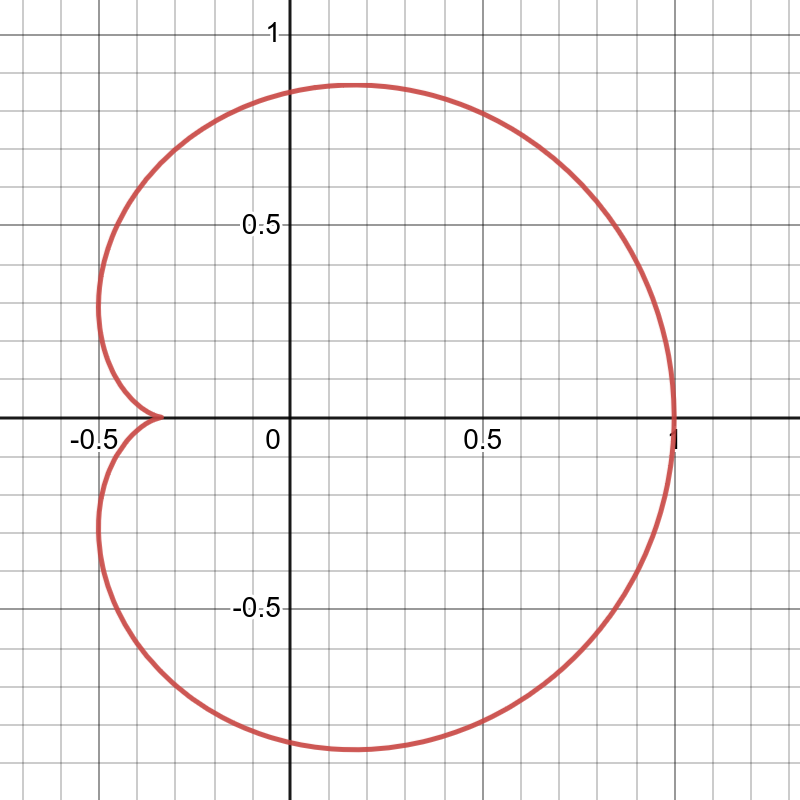
\[27X^{4}+54X^{2}Y^{2}-18X^{2} -8X + 27Y^{4}-18Y^{2}-1=0.\]

就是心脏线的隐函数表示。不信？在 Desmos 里面画出来看看！

注记

这篇文章主要覆盖了 Greg Egan 博文的前半部分，他的后半部分内容我觉得有点放飞自我，也没怎么仔细看。

虽然我们用 sympy 的实验很成功，但注意并不是所有情况下都能得到焦散曲线（比如光源位于抛物线的焦点时，反射光线都是平行的），而且对复杂的曲线 sympy 算起来非常慢。

我研究生的时候上过计算机代数的课程，当时用的教学软件是 Maple。Maple 编程是很不方便的，所以我其实没有多少计算机代数的编程经验。我之前一直觉得 sympy 运行又慢，输出的表达式也不够简化，所以不太愿意用它。这次实验有点刷新我对 sympy 的认知。我还记得当时课程要求每人提交一份读书报告，我写的是 Ideals, Varieties, and Algorithms 的笔记，但毕业多年以来这还是我第一次用到 Gröbner 基！

我写这篇文章的时候正好临近情人节，所以我在想有没有什么曲线的焦散能给出 爱心曲线：

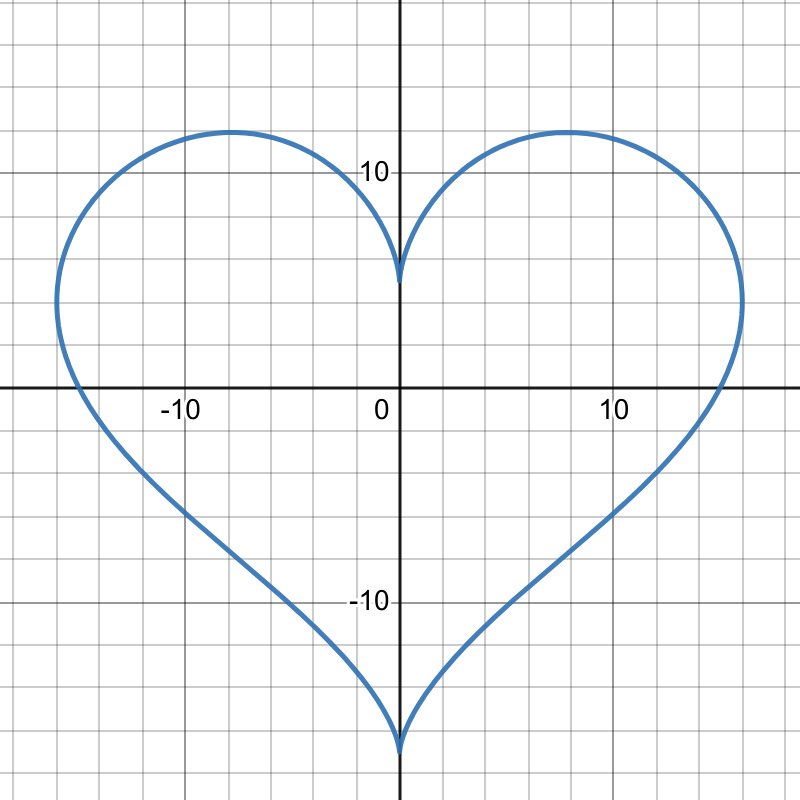
于是我找到了 这篇文章。不过看起来里面给出的结论计算量很大，很难用在爱心线上（也许是我错了）。

另一个发散思考的角度是，如果这个咖啡杯是放在 Poincaré 双曲圆盘里面，它的焦散是怎么样的。这个时候光走的是双曲空间中的测地线（与单位圆正交的圆弧），所以看起来有点难办。但是如果我们先从 Beltrami-Klein 模型入手（测地线是直线），就会发现一切和我们上面的分析是一样的。所以 Poincaré 圆盘里的真实焦散和我们上面计算的焦散只差一个从 Beltrami-Klein 模型到 Poincaré 模型的变换。

下一篇：Möbius 变换与球的刚体运动