本文的想法源自 Roice Nelson 的 shadertoy 项目，我觉得他的创意很棒，就是效果有点糙，于是 动手改进了一番。乍一看，这个动画的场景很简单，其实它背后的数学并不平凡。

这个动画从三个角度了演示 Möbius 变换，这三个角度是密切相关的：

1. Möbius 变换作为扩充复平面 \(\hat{\mathbb{C}}\) 到自身的全纯函数。
2. Möbius 变换作为 Riemann 球面 \(S^2\) 到自身的全纯函数。
3. Möbius 变换作为上半双曲空间中的等距变换。

本文只作概括性的介绍，并不展开详细的数学证明。读者可以参考下面的资料：

1. 维基百科.
2. Needham (1997) .
3. Mumford, Series, and Wright (2002), chapter 3.
4. Palka (1991), chapter IX, section 2.

本文的动画应该可以帮助你更好地理解这些资料中的内容。

预备知识之正交圆族

设 \(z_1,z_2\) 是复平面上的两点，我们考虑两个不同的圆族 \(\mathcal{C}_1\) 和 \(\mathcal{C}_2\)：

1. \(\mathcal{C}_1\) 由所有同时过 \(z_1\) 和 \(z_2\) 的圆组成（包含过 \(z_1,z_2\) 的直线）。
2. \(\mathcal{C}_2\) 由所有使得 \(z_1\) 和 \(z_2\) 关于 \(C\) 互为反演点的圆 \(C\) 组成（包含线段 \([z_1,z_2]\) 的垂直平分线）。

则圆族 \(\mathcal{C}_1\) 中的任何圆 \(C_1\) 与 \(\mathcal{C}_2\) 中的任何圆 \(C_2\) 正交（交点处的切线互相垂直）。

我们将考察当 \(z_1,z_2\) 是一个 Möbius 变换 \(M\) 的两个不动点时，\(M\) 作用在 \(\mathcal{C}_1\) 和 \(\mathcal{C}_2\) 上的效果。

Möbius 变换的共轭分类

一个 Möbius 变换 \(M\) 是一个分式线性变换，它将扩充复平面 \(\hat{\mathbb{C}}\) 一对一地映射为自身： \[M(z) = \frac{az+b}{cz+d},\quad a,b,c,d\in\mathbb{C},ad-bc\ne0, z\in \hat{\mathbb{C}}.\] 所有的 Möbius 变换构成一个群 \({\rm PSL}_2(\mathbb{C})\)。

我们称两个 Möbius 变换 \(M_1,M_2\) 是共轭的，当且仅当存在 \(g\in{\rm PSL}_2(\mathbb{C})\) 使得 \[M_1=gM_2 g^{-1}.\]

可以证明，在共轭的意义下，任何非恒等元的 Möbius 变换都属于下面四种类型之一：

1. \(M\) 称作是抛物型的 (parabolic)，如果它共轭于平移：\(z\to z+1\)。这时 \(M\) 在 \(\hat{\mathbb{C}}\) 上仅有一个不动点。
2. \(M\) 称作是椭圆型的 (elliptic)，如果它共轭于旋转：\(z\to e^{i\theta}z\)，其中 \(\theta\in\mathbb{R}\) 且 \(\theta\ne0\)。这时 \(M\) 在 \(\hat{\mathbb{C}}\) 上有两个不动点。
3. \(M\) 称作是双曲型的 (hyperbolic)，如果它共轭于缩放：\(z\to\lambda z\)，其中 \(\lambda>0\) 是实数且不为 1。这时 \(M\) 在 \(\hat{\mathbb{C}}\) 上有两个不动点。
4. \(M\) 称作是斜航型的 (loxodromic)，如果它共轭于一个缩放和一个旋转的复合：\(z\to cz\)，其中 \(c\in\mathbb{C}\setminus \mathbb{R}\)。这时 \(M\) 在 \(\hat{\mathbb{C}}\) 上有两个不动点。

我们把形如 \(z\to z+a\) 和 \(z\to\lambda z\) 的变换称作特殊位置的变换，前者是抛物型的，以 \(\infty\) 为唯一不动点，后者包含了所有非抛物型的变换，它的两个不动点是 \(0\) 和 \(\infty\)。这两种 Möbius 变换具有简单的表现形式，并且它们在两个圆族上的作用也很容易分析，所以在研究每种类型的变换时，我们都先考虑这种简单的形式，然后再通过取共轭扩展到一般的情形。

1. 抛物型

我们先考察最简单的抛物型变换 \(z\to z+1\)。

这时唯一的不动点是 \(\infty\)，\(\mathcal{C}_1\) 是直线族 \(\{y=k\mid k\in\mathbb{R}\}\)，\(\mathcal{C}_2\) 是直线族 \(\{x=l\mid l\in\mathbb{R}\}\)。\(M\) 保持 \(\mathcal{C}_1\) 中的每条直线不变，把 \(\mathcal{C}_2\) 中的每条直线变成同族中的另一条直线：

由动画可见所有点都向着不动点 \(\infty\) 的方向「前进」。

对一般的抛物型变换 \(M\) 且 \(M\) 的唯一不动点 \(z_0\) 有限的情形，结论仍然类似：圆族 \(\mathcal{C}_1\) 中的圆都在 \(z_0\) 处相切且共用同一条切线 \(\ell_1\)，圆族 \(\mathcal{C}_2\) 也都在 \(z_0\) 处相切且共用同一条切线 \(\ell_2\)，\(\ell_1\) 和 \(\ell_2\) 互相垂直：

由动画可见左右两侧的圆在旋转，但是圆本身保持不变，它们是圆族 \(\mathcal{C}_1\)；上下两侧的圆在「扩散」，它们是圆族 \(\mathcal{C}_2\)。可以证明对任何 \(z\in\mathbb{C}\) 都有 \(\lim\limits_{n\to\infty}M^n(z)=z_0\)，即任何点在 \(M\) 反复作用下的轨迹都朝着 \(z_0\) 的位置移动。

在 Indra’s pearls 一书中，把 \(\mathcal{C}_1\) 和 \(\mathcal{C_2}\) 形象地比喻为两组「扇贝壳」：

2. 椭圆型

我们先考察最简单的椭圆型变换 \(z\to e^{i\theta}z\)。

这时两个不动点是 \(0\) 和 \(\infty\)。圆族 \(\mathcal{C}_1\) 由所有过 \(0\) 的直线组成，\(\mathcal{C}_2\) 由所有以 \(0\) 为中心的同心圆组成。\(M\) 是个旋转，所以会把 \(\mathcal{C}_1\) 中的直线变成同族的另一条直线，同时保持 \(\mathcal{C}_2\) 中的每个圆不变：

对两个不动点 \(z_1\) 和 \(z_2\) 都有限的情形，结论同样成立，\(M\) 保持 \(\mathcal{C}_2\) 中的每个圆不变，把 \(\mathcal{C}_1\) 中的每个圆变为同族中的另一个圆：

3. 双曲型

与椭圆变换 \(z\to e^{i\theta}z\) 的情形类似，\(z\to\lambda z\) 也以 \(0\) 和 \(\infty\) 为不动点，但是圆族 \(\mathcal{C}_1\) 和 \(\mathcal{C}_2\) 的运动方式发生了互换：这次 \(\mathcal{C}_1\) 中的每条直线在放缩下保持不变，\(\mathcal{C}_2\) 中的每个圆在放缩下变成同族的另一个圆：

对两个不动点 \(z_1\) 和 \(z_2\) 都有限的双曲变换，结论仍然成立，圆族 \(\mathcal{C}_1\) 中的每个圆保持不变，\(\mathcal{C}_2\) 中的每个圆被变成同族的另一个：

这时在 \(M\) 的作用下 \(z_1\) 和 \(z_2\) 一个是「源点」，另一个是「汇点」，轨迹从源点源源不竭地发出，汇聚到汇点中。

4. 斜航型

仍然先看 \(z\to cz\) 的情形。

这时不动点是 \(0\) 和 \(\infty\)，\(M\) 把圆族 \(\mathcal{C}_1\) 中的每个圆变为同族中的另一个圆，同样地也把圆族 \(\mathcal{C}_2\) 中的每个圆变为同族中的另一个圆，所以斜航型的变换没有不变圆：

这时平面上一点 \(z\) 在 \(M\) 的反复作用下的轨迹是一条形如「旋臂」的曲线，方程为 \(\gamma(t)=c^tz\)，这是一条对数螺线 (spiral)，其与 \(\mathcal{C}_1\) 和 \(\mathcal{C}_2\) 的夹角都是常数。

这个结论对一般的斜航型变换也成立：

由于斜航型变换包含双曲变换作为组成成分，因此看起来它也有一个源点和一个汇点。这时任意一点 \(z\) 在 \(M\) 的反复作用下的轨迹是一条双螺线 (double spiral)，其与 \(\mathcal{C}_1\) 和 \(\mathcal{C}_2\) 的夹角仍然都是常数 （Möbius 变换是保角的）。

判断 Möbius 变换 \(M\) 具体属于哪一类可以根据其迹的平方 \(\mu=(a+d)^2\) 来判断（当然，需要把 \(M\) 归一化使得 \(ad-bc=1\)）：

1. \(M\) 是抛物型的当且仅当 \(\mu=4\)。
2. \(M\) 是椭圆型的当且仅当 \(0\leq\mu<4\)。
3. \(M\) 是双曲型的当且仅当 \(\mu>4\)。
4. \(M\) 是斜航型的当且仅当 \(\mu<0\) 或者 \(\mu\notin\mathbb{R}\)。

斜航 (loxodromic) 是什么意思？

斜航这个词听起来好像和船的航行有关，怎么就用来给 Möbius 变换分类了呢？这里面肯定有故事，值得扒一扒。

斜航线 (loxodrome) 指的是地球上的一条航行路径，其在每个点处的切线与过该点的经线的夹角为定值。比如说，如果船始终朝着东北方向 30 度行驶，走过的轨迹就是一条斜航线。Loxodrome 最初是一个希腊词，loxos 的意思是 oblique，即倾斜的，dromos 意为 bearing，方位的意思，后来拉丁化以后成为现在的样子。葡萄牙数学家 Pedro Nunes (1492-1577) 第一个认识到斜航线并非两点之间最短路径，而且它无限接近但永不可能到达极点。

在大航海的时代，没有卫星导航，只能靠罗盘或者星座来标识船的航向，而星座的方法在遇到恶劣天气的时候又不能使用，只有罗盘是最可靠的方法。理论上地球表面两点之间的最短路径是过球心的大圆，但罗盘只能定出经线的方向 （原理是地球的磁极和南北极近似重合），这二者的夹角不是固定的，要保持沿着大圆的弧走就必须不停调整船的航向，但现实中的船不可能一直有人守在船舵处调整方向，一般是事先定好航向以后接下来的若干天都沿着这个方向走，所以在一定路程内船实际上走的是斜航线。

荷兰地图学家墨卡托 (Mercator) 据此于 1569 年提出了墨卡托地图，将地球投影至墨卡托地图是一个保角变换，即曲线的夹角保持不变。不仅如此，球面上的斜航线在墨卡托地图中成为一条直线：

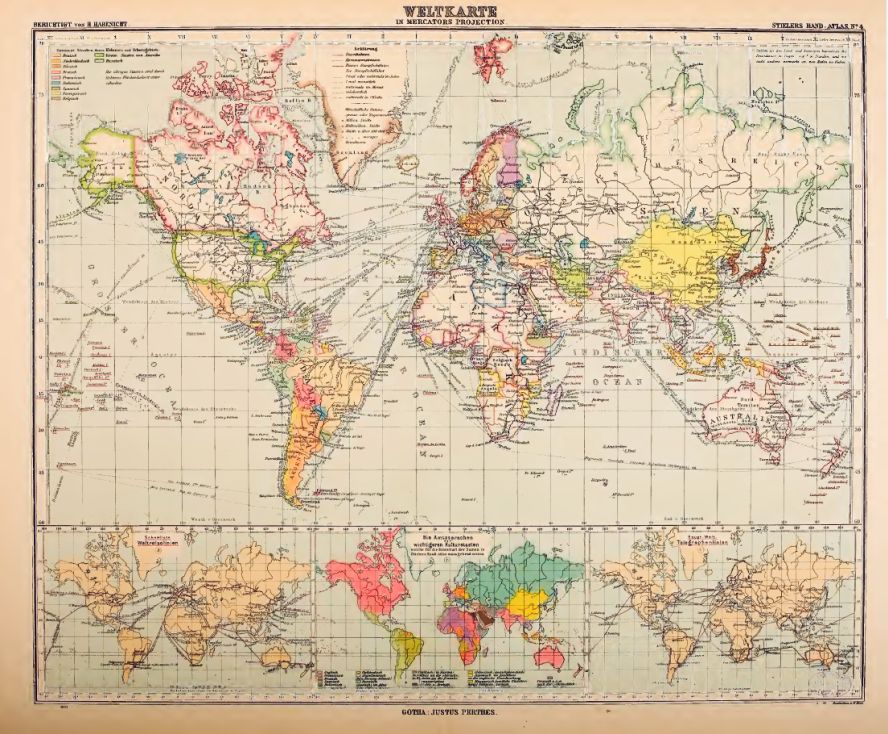
所以要从地球上的 \(A\) 点航向到 \(B\) 点，只要找到它们在墨卡托地图上的对应点 \(A',B'\)，算出地图上的直线 \(A'B'\) 与经线的夹角 \(\theta\)，航行时只要让罗盘与经线一直保持角度为 \(\theta\) 就可以按照斜航线从 \(A\) 航行到 \(B\) 了。这个路径虽不是最短，但是好在不容易迷失航向。

那这和 Möbius 变换有什么关系呢？

Möbius 变换作用在 Riemann 球面上

由于 Möbius 变换都是扩充复平面 \(\hat{\mathbb{C}}\) 到 \(\hat{\mathbb{C}}\) 的自同构，而 \(\hat{\mathbb{C}}\) 在球极投影下等同于 Riemann 球面 \(S^2\)，所以 Möbius 变换也都是 Riemann 球面的自同构。我们来看看 Möbius 变换作用在 Riemann 球面上是什么样子的。

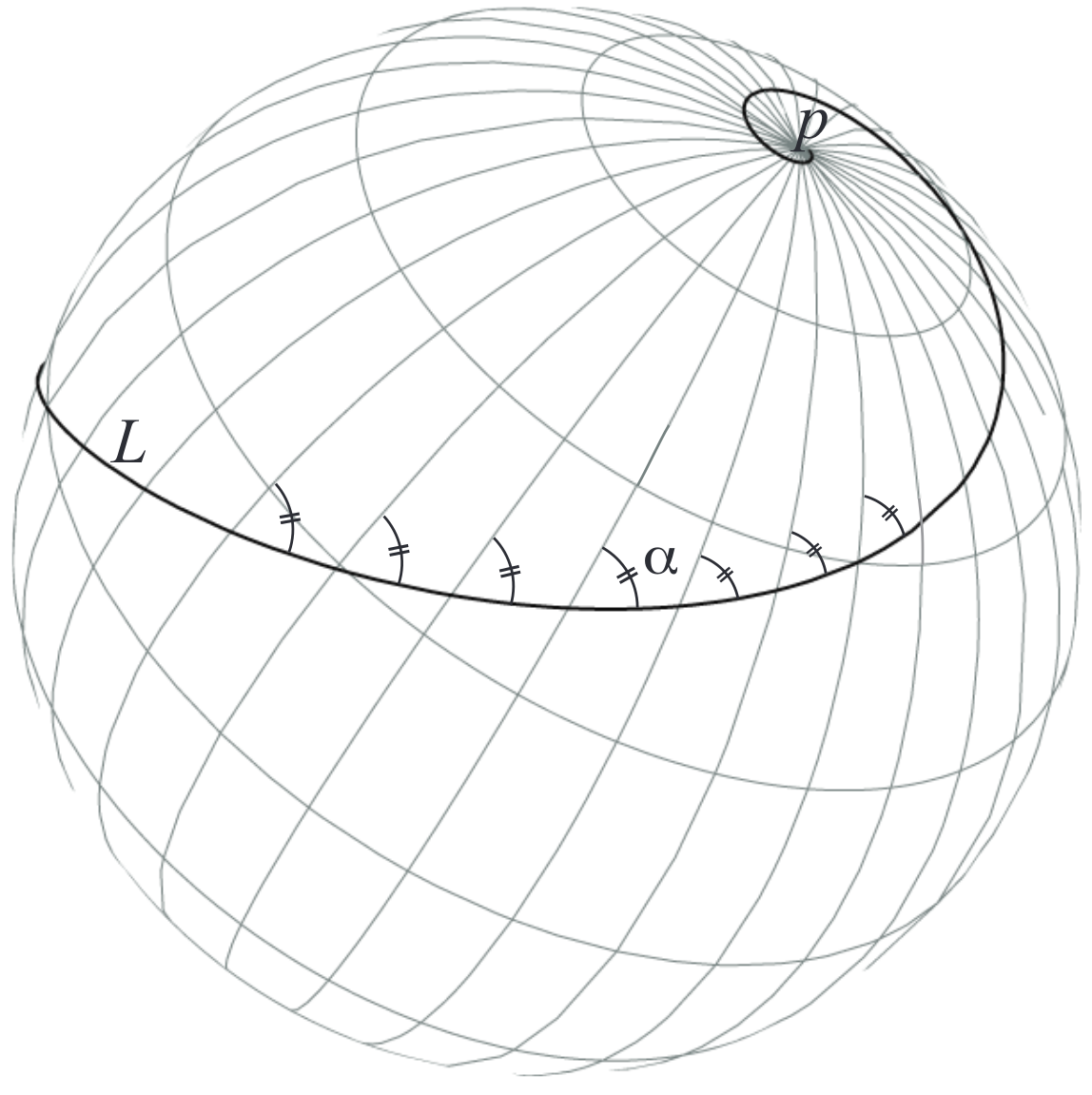
这是一个作用在 Riemann 球上的斜航型变换：

我来解释一下这个动画的含义：从动画可见 Riemann 球面上有一对源点和汇点，这对源点和汇点可以理解为球面的「北极」和「南极」，它们在球极投影下对应于 \(M\) 在扩充复平面上的两个不动点。当这两个不动点分别是原点和无穷远点时，这两个极点就是通常意义下的北极和南极。这时球面上的「经线」是所有过两个极点的大圆，在球极投影下它们对应于同时过两个不动点的圆族 \(\mathcal{C}_1\)；球面上的「纬线」是所有与经线正交的圆，在球极投影下它们对应于反演圆族 \(\mathcal{C}_2\)，球面上每个点的轨迹是对数螺线轨迹在逆球极投影下在球面上的对应曲线，这条曲线与经线纬线的夹角都是常数（因为球极投影是保角的），从而是一条斜航线！

提示：这个动画有两种解释，它既可以看作是一个抛物型变换在 Riemann 球面上作用的效果，也可以看作是一个上半双曲空间中的 horosphere 在抛物型变换下作用的效果。horosphere 是指上半双曲空间中与无穷远平面 \(z=0\) 相切的球，其半径为无穷大。Möbius 变换在上半双曲空间上的作用见下一节。

Möbius 变换作为上半双曲空间的等距

上半双曲空间 \(\mathbb{H}_3\) 的定义为 \[\mathbb{H}_3 = \{(x,y,t)\in\mathbb{R}^3\ |\ t>0\}.\] 这个空间中的度量是双曲度量：

\[\mathrm{d}s=\frac{(\mathrm{d}x)^2+(\mathrm{d}y)^2+(\mathrm{d}t)^2}{t}.\]

注意 \(xy\) 平面，即复平面不属于 \(\mathbb{H}_3\)，它是 \(\mathbb{H}_3\) 的无穷远边界，\(\mathbb{H}_3\) 中任何一点到 \(xy\) 平面的距离是无穷大。

一个复分析教材中不太常讲到的事实是：任何 Möbius 变换都可以唯一地扩展为 \(\mathbb{H}_3\) 的一个等距变换 \(\overline{M}\)，此即所谓的 Poincaré Extension。这个扩展用四元数来描述的话很简单：设 \[M\colon\ z\to\frac{az+b}{cz+d},\quad ad-bc=1.\] 是任一 Möbius 变换。注意我们这里要求 \(ad-bc\) 的值是 1，其实任何非零实数都可以。这是可以做到的，因为给 Möbius 变换中的 \(a,b,c,d\) 同时乘以一个非零复数并不改变这个变换，所以同时乘以 \(1/\sqrt{ad-bc}\) 就可以使得 \(ad-bc=1\)。

对 \(p=(x,y,t)\in\mathbb{H}^3\)，令 \(q=x+yi+tj\) 为与 \(p\) 对应的四元数，定义 \[\overline{M}(p) = (aq+b)(cq+d)^{-1}.\] 这里的运算都是在四元数体中进行。则 \(\overline{M}(p)\) 是 \(\mathbb{H}_3\) 到自身的等距，并且它限制在 \(xy\) 平面上与 \(M\) 的作用一致。

关于 Poincaré Extension 读者可以参考 (Beardon 1995, vol. 91, secs. 3.3, 4.1)。

我们还能像上面那样用动画演示 Möbius 变换 \(\overline{M}\) 在 \(\mathbb{H}_3\) 上的作用吗？可以！比如下图是一个形如 \(z\to cz\) 的斜航型变换扩展到 \(\mathbb{H}_3\) 后作用在一个圆柱体上的效果：

你可能要问了：这明明是个圆锥体，你怎么说它是圆柱体呢？是不是笔误了啊？

其实是因为我们现在是在双曲空间里看待它，在双曲度量下，锥面上所有点到 \(t\) 轴的距离都是一样的，实际上如果设锥的顶角为 \(2\alpha\)，则锥面上任何一点到 \(t\) 轴的双曲距离 \(d\) 满足（见 (Beardon 1995, vol. 91, sec. 7.9.1)） \[\sinh d\cdot \cot\alpha = 1.\] 即 \(d\) 是定值。所以虽然在 \(\mathbb{R}^3\) 中它是一个锥体，但是在 \(\mathbb{H}_3\) 中它其实是圆柱体。

你可以看到这时 \(\overline{M}\) 有两个不动点，都位于无穷远边界上，这样的点叫做「理想点」。两个不动点之间的连线构成圆柱的轴。两个不动点一个是源点，一个是汇点，空间中的点在变换的作用下远离源点，趋向汇点。

对于一般的斜航型变换 \(M\)，且其两个不动点都是扩充复平面上的有限点时，\(M\) 在 \(\mathbb{H}_3\) 上的扩展 \(\overline{M}\) 仍然保持一个 \(\mathbb{H}_3\) 中的圆柱体不变：

这个曲面叫做 Dupin cyclide，它的两个端点恰好是 \(M\) 的两个不动点。但在双曲空间中它其实是一个圆柱体，由于其两端落在无穷远平面上，因此也是无限长的。圆柱体的轴是连接两个端点的测地线。如果 \(M\) 是椭圆型的话，那么 \(\overline{M}\) 将该圆柱绕着轴旋转：

这些动画是怎么生成的？

我以 Dupin cyclide 的动画为例子来说明动画的绘制过程。

一个非抛物型的变换 \(M\) 总是可以表示为 \(M = gM_\lambda g^{-1}\) 的形式，其中 \(M_\lambda=z\to\lambda z\)。我这里的 \(g\) 取的是 \[g^{-1}(z)=\frac{z-1}{z+1}.\] 注意我这里写的是 \(g^{-1}\)，原因是我们不需要 \(g\) 的显式表达式，相反我们只需要 \(g^{-1}\)。

不难验证 \(g^{-1}(1)=0\) 和 \(g^{-1}(-1)=\infty\)，从而 \(g(0)=1\) 和 \(g(\infty)=-1\)，即 \(g\) 将 \(M_\lambda\) 的不动点 \(\{0,\infty\}\) 分别映射为 \(M\) 的不动点 \(\{1,-1\}\)。\(g\) 同时将 \(M_\lambda\) 对应的圆族 \(\{\mathcal{C}_i,i=1,2\}\) 映射为 \(M\) 的圆族 \(\{g(\mathcal{C}_i),i=1,2\}\)。

\(g\) 当然也可以扩展为 \(\mathbb{H}_3\) 的等距，我们把扩展以后的 \(g\) 仍然记作 \(g\)。

由 \(M = gM_\lambda g^{-1}\) 可得 \[Mg(\mathcal{C}_i) = gM_\lambda (\mathcal{C}_i),\quad i=1,2.\] 左边的 \(Mg(\mathcal{C}_i)\) 是我们真正想绘制的 \(M\) 在其自己的圆族 \(g(\mathcal{C}_i)\) 上的作用，这等价于绘制右边的 \(gM_\lambda(\mathcal{C})_i\)。\(M_\lambda(\mathcal{C}_i)\) 很好画，就是把一些同心圆和过原点的直线旋转或者放缩一下；但是它前面加了一个畸变 \(g\)。为此我们只要用 \(g^{-1}\) 作用在当前场景的物体上，把它们「去畸变」即可。所以在动画中，我其实根本没有计算 Dupin cyclide 的任何显式或者隐式的曲面方程，而是直接用 \(g^{-1}\) 作用在场景上。由于 \(g^{-1}\) 是 \(\mathbb{H}_3\) 上的等距，它一定会把连接 \(\{\pm1\}\) 的测地线映射为连接 \(\{0,\infty\}\) 的测地线，即锥面。换言之，判断场景中的一个点 \(p\) 是不是落在 Dupin cyclide 上，只要判断 \(g^{-1}(p)\) 是不是落在锥面上。这就好办了。

抛物的情形更简单一些，可以用 \(g(z)=1/z\) 把位于无穷远的不动点变到原点。

动画使用的是 GLSL 语言和 raymarching 的技术。我在 Roice 的代码基础上作了许多优化，但肯定还可以更精炼。限于我写 shader 的能力不足，做出更美轮美奂的效果就不指望了 …

严格讲，这些动画其实还是尝试在 Euclidean 空间中去观察双曲空间中的对象，因为 raymarching 技术假定的是光走直线，但在双曲空间中光一般不走直线，所以我们这里看到的效果与真实的生活在双曲空间中的“外星人”所看到的还是有差别的。

References

上一篇：Todd-Coxeter 算法和 3D/4D 均匀多胞体

下一篇：碉堡的小程序：用 Python 制作演示各种算法的 GIF 动画