问题： 假设你是一位大龄男士，准备参加 100 场相亲 （别介意具体数字）。你打算依次与每个女士 \(i\) 约会，然后根据印象给她打一个分数 \(X_i\)，\(X_i\) 的值介于 \([0,1]\) 之间。如果你对女士 \(i\) 很满意，那么就和她结婚，否则就放弃她，参加下一场相亲，当然拒绝了人家可就没有回头的机会了。如果你拒绝了前 99 位女士，那么不论第 100 次相亲结果如何你都只能和最后这位女士结婚。在相亲之前，你对这些女士的情况一无所知，所以姑且假定她们的分数 \(X_i\) 都是 \([0,1]\) 上均匀分布的独立的随机变量。问题是：应该采取怎样的相亲策略，才能娶到你最中意的女士？
今天的问题是群表示论在物理中的一个小应用：
问题： 平面上有三个质量均为 \(m\) 的质点 \(A,B,C\)，它们位于正三角形的三个顶点。质点之间两两由弹簧相连，三个弹簧完全一样。弹簧质量忽略不计。
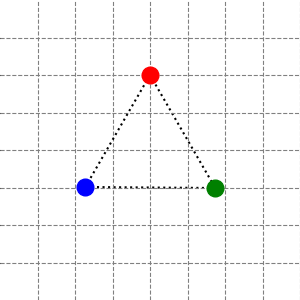
初始时所有质点都处于静止状态，弹簧之间没有张力。假设给这三个质点分别施加一个初始速度，使这三个质点在平面内作刚体运动，不考虑任何摩擦力和空气阻力，那么这个系统的简正模式 (normal mode) 是什么？
这里 简正模式 的含义是所有质点按照一个共同的频率和固定的相位关系相对于各自的平衡位置作简谐振动。
著名概率学家 Feller 在他的名著 “An introduction to probability and its applications” 中提到了这样一个实验：
问题： 重复抛掷一枚均匀的硬币，用 H
代表正面向上，T 代表背面向上，一直到连续出现 6 次
H 为止。这里连续 6 个 Ｈ 组成的模式记作
HHHHHH，所需要抛掷硬币的次数叫做等待时间。等待时间是一个随机变量，最小值是
6，最大值可以是无限。Feller 问：等待时间的均值是多少？
这个问题可以用 Markov 链来解，但是非常繁琐。香港中文大学李硕彦教授在他的论文 (Li 1980) 中用离散鞅的知识给出了一个简洁而巧妙的解法，本文就来介绍他的方法。
今天的问题源自中世纪威尔士人的故事集《Mabinogion》中的一段：
一个男孩来到了一个美丽的山谷，有一条小河在谷中流淌。他看到河一边的草地上有一群黑绵羊，另一边的草地上有一群白绵羊。羊群被施以一种魔法：每个时刻都恰有一只绵羊发出咩咩的叫声。如果发出叫声的是白绵羊，就会有一只黑绵羊趟过小河跑过来并且变成白绵羊；如果发出叫声的是黑绵羊，则会有一只白绵羊趟过小河跑过去并且变成黑绵羊。每个时刻发出叫声的绵羊是完全随机的，整个过程没有绵羊出生或者死亡，一直持续到所有绵羊都变成同一种颜色为止。
问题是这样的：
问题： 如果男孩可以选择在初始时刻 \(0\)，或者是每个魔法时刻 \(1,2,\ldots\) 结束后将任意数量的白绵羊赶出山谷，那么为了最终得到尽可能多的黑绵羊，他应该采取怎样的策略？
本文的问题出自 Williams 的教材 Probability with Martingales，虽然不算很难但是综合使用了许多知识，展示了抽象的鞅理论其实有着丰富多彩的应用。
问题： 一艘太空船正在宇宙中做星际航行时，飞船的控制系统出了故障，飞船不能正常地进行空间跳跃，而是只能预先设定一个距离，然后以此距离进行一次方向完全随机的跳跃。现在飞船想要返回太阳系。假设太阳系的半径是 \(r\)，发生故障时飞船与太阳的距离为 \(R>r\)。好消息是在每个时刻，飞船能够知道自身与太阳系的距离。
求证：不论采用怎样的跳跃策略，飞船返回太阳系的概率都小于 \(r/R\)；但是对任何 \(\epsilon>0\)，可以采取适当的策略，使得飞船返回太阳系的概率大于 \((r-\epsilon)/R\)，即 \(r/R\) 是最优概率。这个最优策略是什么？
当前网速较慢或者你使用的浏览器不支持博客特定功能，请尝试刷新或换用Chrome、Firefox等现代浏览器